
 過拋物線焦點垂直于對稱軸的弦叫做拋物線的通徑.如圖,已知拋物線y2=2px(p>0),過其焦點F的直線交拋物線于A(x1,y1)、B(x2,y2)兩點,過A、B作準線的垂線,垂足分別為A1、B1.
過拋物線焦點垂直于對稱軸的弦叫做拋物線的通徑.如圖,已知拋物線y2=2px(p>0),過其焦點F的直線交拋物線于A(x1,y1)、B(x2,y2)兩點,過A、B作準線的垂線,垂足分別為A1、B1.| p2 |
| 4 |
| p2 |
| 4 |
| FA1 |
| FB1 |
| FA1 |
| FB1 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p2 |
| 4 |
| p |
| 2 |
|
| k |
| 2p |
| kp |
| 2 |
| y12 |
| 2p |
| y22 |
| 2p |
| p2 |
| 4 |
| p2 |
| 4 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
| FA1 |
| FB1 |
| FA1 |
| FB1 |
| FA1 |
| FB1 |


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| d |
| 3 |
查看答案和解析>>
科目:高中數學 來源:上海市長寧區2012屆高三4月教學質量檢測(二模)數學理科試題 題型:044
設拋物線C:y2=2px(p>0)的焦點為F,過F且垂直于x軸的直線與拋物線交于P1,P2兩點,已知|P1P2|=8.
(1)求拋物線C的方程;
(2)設m>0,過點M(m,0)作方向向量為![]() =(1,
=(1,![]() )的直線與拋物線C相交于A,B兩點,求使∠AFB為鈍角時實數m的取值范圍;
)的直線與拋物線C相交于A,B兩點,求使∠AFB為鈍角時實數m的取值范圍;
(3)①對給定的定點M(3,0),過M作直線與拋物線C相交于A,B兩點,問是否存在一條垂直于x軸的直線與以線段AB為直徑的圓始終相切?若存在,請求出這條直線;若不存在,請說明理由.
②對M(m,0)(m>0),過M作直線與拋物線C相交于A,B兩點,問是否存在一條垂直于x軸的直線與以線段AB為直徑的圓始終相切?(只要求寫出結論,不需用證明)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市長寧區高三4月教學質量檢測(二模)理科數學試卷(解析版) 題型:解答題
(本題滿分18分)本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分其中①6分、②2分。
設拋物線
 的焦點為
的焦點為 ,過
,過 且垂直于
且垂直于 軸的直線與拋物線交于
軸的直線與拋物線交于 兩點,已知
兩點,已知 .
.
(1)求拋物線 的方程;
的方程;
(2)設 ,過點
,過點 作方向向量為
作方向向量為 的直線與拋物線
的直線與拋物線 相交于
相交于 兩點,求使
兩點,求使 為鈍角時實數
為鈍角時實數 的取值范圍;
的取值范圍;
(3)①對給定的定點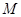
 ,過
,過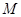 作直線與拋物線
作直線與拋物線 相交于
相交于 兩點,問是否存在一條垂直于
兩點,問是否存在一條垂直于 軸的直線與以線段
軸的直線與以線段 為直徑的圓始終相切?若存在,請求出這條直線;若不存在,請說明理由。
為直徑的圓始終相切?若存在,請求出這條直線;若不存在,請說明理由。
②對 ,過
,過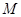 作直線與拋物線
作直線與拋物線 相交于
相交于 兩點,問是否存在一條垂直于
兩點,問是否存在一條垂直于 軸的直線與以線段
軸的直線與以線段 為直徑的圓始終相切?(只要求寫出結論,不需用證明)
為直徑的圓始終相切?(只要求寫出結論,不需用證明)
查看答案和解析>>
科目:高中數學 來源:2012年上海市長寧區高考數學二模試卷(理科)(解析版) 題型:解答題
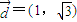 的直線與拋物線C相交于A,B兩點,求使∠AFB為鈍角時實數m的取值范圍;
的直線與拋物線C相交于A,B兩點,求使∠AFB為鈍角時實數m的取值范圍;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com