
【題目】某單位為綠化環境,移栽了甲、乙兩種大樹各2株.設甲、乙兩種大樹移栽的成活率分別為 ![]() 和
和 ![]() ,且各株大樹是否成活互不影響.求移栽的4株大樹中:
,且各株大樹是否成活互不影響.求移栽的4株大樹中:
(1)兩種大樹各成活1株的概率;
(2)成活的株數ξ的分布列與期望.
【答案】
(1)解:設Ak表示甲種大樹成活k株,k=0,1,2
Bl表示乙種大樹成活1株,1=0,1,2
則Ak,Bl獨立.由獨立重復試驗中事件發生的概率公式有
P(Ak)=C2k( ![]() )k(
)k( ![]() )2-k,P(Bl)=C21(
)2-k,P(Bl)=C21( ![]() )l(
)l( ![]() )2-l.
)2-l.
據此算得P(A0)= ![]() ,P(A1)=
,P(A1)= ![]() ,P(A2)=
,P(A2)= ![]() .
.
P(B0)= ![]() ,P(B1)=
,P(B1)= ![]() ,P(B2)=
,P(B2)= ![]() .
.
所求概率為P(A1B1)=P(A1)P(B1)= ![]() ×
× ![]() =
= ![]() .
.
(2)解:ξ的所有可能值為0,1,2,3,4,且
P(ξ=0)=P(A0B0)=P(A0)P(B0)= ![]() ×
× ![]() =
= ![]() ,
,
P(ξ=1)=P(A0B1)+P(A1B0)= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
P(ξ=2)=P(A0B2)+P(A1B1)+P(A2B0)= ![]() ×
× ![]() +
+ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
P(ξ=3)=P(A1B2)+P(A2B1)= ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() .
.
P(ξ=4)=P(A2B2)= ![]() ×
× ![]() =
= ![]() .
.
綜上知ξ有分布列
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
從而,ξ的期望為
Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() +4×
+4× ![]() =
= ![]() (株).
(株).
【解析】(1)根據題意結合已知條件利用獨立重復試驗中事件發生的概率公式![]() 代入數值求出結果即可,再結合概率的乘法原理求出結果即可。(2)根據題意利用概率的乘法原理以及獨立重復試驗中事件發生的概率公式分別求出隨機變量的各個取值下的概率列表即可,再根據數學期望的公式計算出結果即可。
代入數值求出結果即可,再結合概率的乘法原理求出結果即可。(2)根據題意利用概率的乘法原理以及獨立重復試驗中事件發生的概率公式分別求出隨機變量的各個取值下的概率列表即可,再根據數學期望的公式計算出結果即可。


科目:高中數學 來源: 題型:
【題目】已知數列![]() 、
、![]() ,其中,
,其中, ![]() ,數列
,數列![]() 滿足
滿足![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)是否存在自然數![]() ,使得對于任意
,使得對于任意![]() 有
有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(3)若數列![]() 滿足
滿足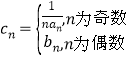 ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com