
如圖,在四棱錐P-ABCD中,PA⊥平面ABCD,E為BD的中點,G為PD的中點,△DAB≌△DCB,EA=EB=AB=1,PA=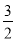 ,連接CE并延長交AD于F.
,連接CE并延長交AD于F.
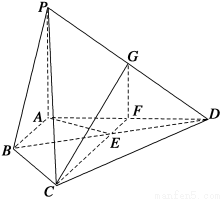
(1)求證:AD⊥平面CFG;
(2)求平面BCP與平面DCP的夾角的余弦值.
(1)見解析(2)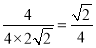
【解析】(1)在△ABD中,因為E是BD中點,所以EA=EB=ED=AB=1,故∠BAD=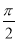 ,∠ABE=∠AEB=
,∠ABE=∠AEB=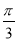 ,
,
因為△DAB≌△DCB,所以△EAB≌△ECB,從而有∠FED=∠BEC=∠AEB=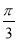 ,
,
所以∠FED=∠FEA.故EF⊥AD,AF=FD,又因為PG=GD,
所以FG∥PA,又PA⊥平面ABCD,所以GF⊥AD,故AD⊥平面CFG.
(2)以A為坐標原點建立如圖所示的坐標系,
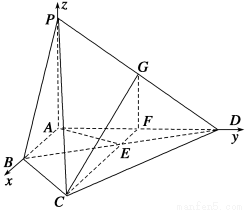
則A(0,0,0),B(1,0,0),C ,D(0,
,D(0,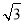 ,0),P
,0),P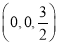 ,故
,故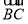 =
= ,
,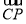 =
= ,
,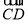 =
= .
.
設平面BCP的法向量n1=(x1,y1,z1),
則
令y1=-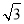 ,則x1=3,z1=2,n1=(3,-
,則x1=3,z1=2,n1=(3,-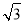 ,2).
,2).
設平面DCP的一個法向量n2=(1,y2,z2),則
解得 即n2=(1,
即n2=(1,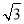 ,2).
,2).
從而平面BCP與平面DCP的夾角θ的余弦值為
cos θ=|cos〈n1,n2〉|=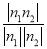 =
=


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練訓練14練習卷(解析版) 題型:填空題
若圓x2+y2=4與圓x2+y2+2ax-6=0(a>0)的公共弦的長為2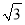 ,則a=________.
,則a=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練訓練10練習卷(解析版) 題型:解答題
正項數列{an}的前n項和Sn滿足: -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.
(1)求數列{an}的通項公式an;
(2)令bn= ,數列{bn}的前n項和為Tn,證明:對于任意的n∈N*,都有Tn<
,數列{bn}的前n項和為Tn,證明:對于任意的n∈N*,都有Tn< .
.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練優化重組卷5練習卷(解析版) 題型:填空題
已知雙曲線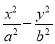 =1(a>0,b>0)的漸近線方程為y=±
=1(a>0,b>0)的漸近線方程為y=±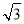 x,則它的離心率為________.
x,則它的離心率為________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練優化重組卷5練習卷(解析版) 題型:選擇題
圓(x+2)2+y2=4與圓(x-2)2+(y-1)2=9的位置關系為( ).
A.內切 B.相交
C.外切 D.相離
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練優化重組卷3練習卷(解析版) 題型:解答題
已知函數f(x)= 的圖象過原點,且關于點(-1,2)成中心對稱.
的圖象過原點,且關于點(-1,2)成中心對稱.
(1)求函數f(x)的解析式;
(2)若數列{an}滿足a1=2,an+1=f(an),試證明數列 為等比數列,并求出數列{an}的通項公式.
為等比數列,并求出數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練優化重組卷2練習卷(解析版) 題型:解答題
在△ABC中,角A,B,C所對的邊分別為a,b,c,已知cos C+(cos A-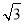 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練x4-1練習卷(解析版) 題型:填空題
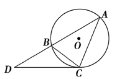
如圖,點A、B、C都在⊙O上,過點C的切線交AB的延長線于點D,若AB=5,BC=3,CD=6,則線段AC的長為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com