
已知函數 的減區間是
的減區間是 .
.
⑴試求m、n的值;
⑵求過點 且與曲線
且與曲線 相切的切線方程;
相切的切線方程;
⑶過點A(1,t)是否存在與曲線 相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
解:⑴ 由題意知: 的解集為
的解集為 ,
,
所以,-2和2為方程 的根,
………………2分
的根,
………………2分
由韋達定理知  ,即m=1,n=0.
………………4分
,即m=1,n=0.
………………4分
⑵ ∵ ,∴
,∴ ,∵
,∵
當A為切點時,切線的斜率  ,
,
∴切線為 ,即
,即 ;
………………6分
;
………………6分
當A不為切點時,設切點為 ,這時切線的斜率是
,這時切線的斜率是 ,
,
切線方程為 ,即
,即
因為過點A(1,-11),  ,∴
,∴
 ,
,
∴  或
或 ,而
,而 為A點,即另一個切點為
為A點,即另一個切點為 ,
,
∴  ,
,
切線方程為  ,即
,即  ………………8分
………………8分
所以,過點 的切線為
的切線為 或
或 . …………9分
. …………9分
⑶ 存在滿足條件的三條切線. …………10分
設點 是曲線
是曲線 的切點,
的切點,
則在P點處的切線的方程為  即
即
因為其過點A(1,t),所以, ,
,
由于有三條切線,所以方程應有3個實根, …………………………11分
設 ,只要使曲線有3個零點即可.
,只要使曲線有3個零點即可.
設  =0, ∴
=0, ∴  分別為
分別為 的極值點,
的極值點,
當 時
時 ,
, 在
在 和
和  上單增,
上單增,
當 時
時 ,
, 在
在 上單減,
上單減,
所以, 為極大值點,
為極大值點, 為極小值點.
為極小值點.
所以要使曲線與x軸有3個交點,當且僅當 即
即 ,
,
解得  .
…………14分
.
…………14分
【解析】略


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源:2010-2011學年山東省濟南市高三4月模擬考試文科數學卷 題型:解答題
已知函數 的減區間是
的減區間是 .
.
⑴試求m、n的值;
⑵求過點 且與曲線
且與曲線 相切的切線方程;
相切的切線方程;
⑶過點A(1,t)是否存在與曲線 相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆山東省高二下學期期末考試數學(文) 題型:解答題
(本小題滿分14分)
已知函數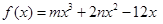 的減區間是
的減區間是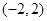 .
.
⑴試求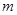 、
、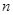 的值;
的值;
⑵求過點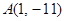 且與曲線
且與曲線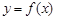 相切的切線方程;
相切的切線方程;
⑶過點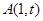 是否存在與曲線
是否存在與曲線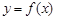 相切的3條切線,若存在,求實數t的取值范圍;若不存在,請說明理由.
相切的3條切線,若存在,求實數t的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
已知函數![]() 的減區間是
的減區間是![]() .
.
⑴試求![]() 、
、![]() 的值;
的值;
⑵求過點![]() 且與曲線
且與曲線![]() 相切的切線方程;
相切的切線方程;
⑶過點![]() 是否存在與曲線
是否存在與曲線![]() 相切的3條切線,若存在,求實數t的取值范圍;若不存在,請說明理由.
相切的3條切線,若存在,求實數t的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
已知函數![]() 的減區間是
的減區間是![]() .
.
⑴試求m、n的值;
⑵求過點![]() 且與曲線
且與曲線![]() 相切的切線方程;
相切的切線方程;
⑶過點A(1,t)是否存在與曲線![]() 相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
相切的3條切線,若存在求實數t的取值范圍;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com