
如圖,已知四棱錐S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一點.
(1)求證:平面EBD⊥平面SAC;
(2)設SA=4,AB=2,求點A到平面SBD的距離;

 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
 如圖,已知四棱錐S-ABCD的底面ABCD是邊長為1的正方形,SA⊥平面ABCD,SA=2,E是側棱SC上的一點.
如圖,已知四棱錐S-ABCD的底面ABCD是邊長為1的正方形,SA⊥平面ABCD,SA=2,E是側棱SC上的一點.查看答案和解析>>
科目:高中數學 來源: 題型:
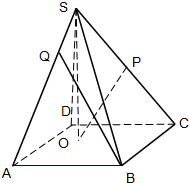 如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.
如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.| AQ |
| 3 |
| 4 |
| AS |
查看答案和解析>>
科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
 (2008•湖北模擬)如圖,已知四棱錐S-ABCD中,△SAD是邊長為a的正三角形,平面SAD⊥平面ABCD,四邊形ABCD為菱形,∠DAB=60°,P為AD的中點,Q為SB的中點.
(2008•湖北模擬)如圖,已知四棱錐S-ABCD中,△SAD是邊長為a的正三角形,平面SAD⊥平面ABCD,四邊形ABCD為菱形,∠DAB=60°,P為AD的中點,Q為SB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 (2010•江西模擬)(如圖)已知四棱錐S-ABCD的底面ABCD是菱形,將面SAB,SAD,ABCD 展開成平面后的圖形恰好為一正三角形S'SC.
(2010•江西模擬)(如圖)已知四棱錐S-ABCD的底面ABCD是菱形,將面SAB,SAD,ABCD 展開成平面后的圖形恰好為一正三角形S'SC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com