
(2006
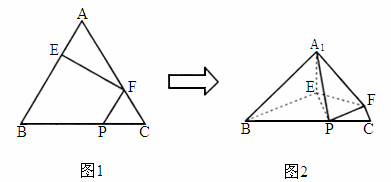
江蘇,19)如下圖,在正三角形ABC中,E、F、P分別是AB、AC、BC邊上的點,滿足AE∶EB=CF∶FA=CP∶PB=l∶2(如圖1).將△AEF沿EF折起到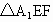 的位置,使二面角
的位置,使二面角 成直二面角,連結
成直二面角,連結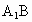 、
、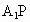 (如圖2).
(如圖2).
(1)
求證: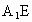 ⊥平面BEP;
⊥平面BEP;
(2)
求直線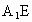 與平面
與平面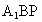 所成角的大小;
所成角的大小;
(3)
求二面角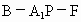 的大小(用反三角函數值表示).
的大小(用反三角函數值表示). |
解析:不妨設正三角形 ABC的邊長為3.(1) 在圖1中,取BE的中點D,連結DF.∵ AE∶EB=CF∶FA=1∶2,∴AF=AD=2,而∠ A=60°,∴△ ADF是正三角形.又AE=DE=1,∴ EF⊥AD.在圖2中,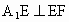 , ,
BE ⊥EF,∴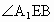 為二面角 為二面角 的平面角. 的平面角.
由題設條件知此二面角為直二面角, ∴ 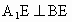 . .
又 BE∩EF=E,∴ ⊥平面BEF, ⊥平面BEF,
即  ⊥平面BEP. ⊥平面BEP.
(2) 在圖2中,∵ 不垂直于 不垂直于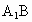 , ,
∴  是平面 是平面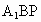 的斜線. 的斜線.
又  ⊥平面BEP,∴ ⊥平面BEP,∴ ⊥BP, ⊥BP,
從而 BP垂直于 在平面 在平面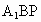 內的射影(三垂線定理的逆定理). 內的射影(三垂線定理的逆定理).
設  在平面 在平面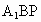 內的射影為 內的射影為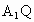 ,且 ,且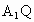 交BP于點Q,則 交BP于點Q,則 就是 就是 與平面 與平面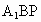 所成的角. 所成的角.
且 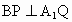 .在△EBP中, .在△EBP中,
∵ BE=BP=2,∠EBP=60°,∴△ EPB是等邊三角形,∴BE=EP.又 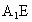 ⊥平面BEP,∴ ⊥平面BEP,∴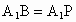 , ,
∴ Q為BP的中點,且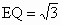 , ,
又 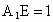 ,在Rt△ ,在Rt△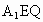 中, 中,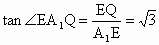 ,∴ ,∴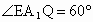 .所以直線 .所以直線 與平面 與平面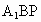 所成的角為60°. 所成的角為60°.
(3) 在圖3中,過F作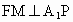 于M,連結QM、QF. 于M,連結QM、QF.
∵ CF=CP=1,∠C=60°,∴△ FCP是正三角形,∴PF=1.又 ∵  ⊥平面BEP, ⊥平面BEP, , ,
∴ 從而 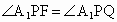 , ② , ②
由①②及 MP為公共邊知△FMP≌△QMP,∴∠ QMP=∠FMP=90°,且MF=MQ,從而∠ FMQ為二面角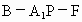 的平面角.在Rt 的平面角.在Rt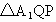 中, 中,
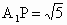 . .
∵ 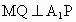 ,∴ ,∴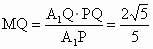 , ,
∴ 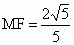 . .
在△ FCQ中,FC=1,QC=2,∠C=60°,由余弦定理得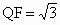 . .
在△ FMQ中,cos∠FMQ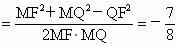 . .
所以二面角  . . |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com