
《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數學著作之一。書中有一道這樣的題目:把100個面包分給五人,使每人成等差數列,且使最大的三份之和的 是較小的兩份之和,則最小1份的大小是
是較小的兩份之和,則最小1份的大小是
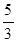
【解析】
試題分析:設五個人所分得的面包為a-2d,a-d,a,a+d,a+2d,(其中d>0);
則,(a-2d)+(a-d)+a+(a+d)+(a+2d)=5a=100,∴a=20;
由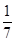 (a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=
(a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=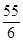
所以,最小的1分為a-2d=20-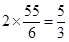 ,故答案為
,故答案為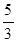 。
。
考點:本題主要考查了等差數列模型的實際應用,解題時應巧設數列的中間項,從而容易得出結果
點評:解決該試題的關鍵是設五個人所分得的面包為a-2d,a-d,a,a+d,a+2d,(d>0);則由五個人的面包和為100,得a的值;由較大的三份之和的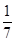 是較小的兩份之和,得d的值;從而得最小的1分a-2d的值.
是較小的兩份之和,得d的值;從而得最小的1分a-2d的值.


科目:高中數學 來源: 題型:
| 1 | 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 7 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省八市高三三月調考理科數學試卷(解析版) 題型:選擇題
《萊因德紙草書》(Rhind
Papyrus)是世界上最古老的數學著作之一,書中有這樣的一道題目:把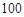 個面包分給
個面包分給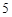 個人,使每人所得成等差數列,且使較大的三份之和的
個人,使每人所得成等差數列,且使較大的三份之和的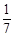 是較小的兩份之和,則最小
是較小的兩份之和,則最小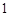 份為( )
份為( )
A.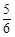 B.
B.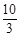 C.
C.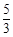 D.
D.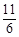
查看答案和解析>>
科目:高中數學 來源:2012-2013學年湖北省八市高三3月聯考文科數學試卷(解析版) 題型:選擇題
《萊因德紙草書》(Rhind
Papyrus)是世界上最古老的數學著作之一,書中有這樣的一道題目:把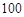 個面包分給
個面包分給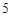 個人,使每人所得成等差數列,且使較大的三份之和的
個人,使每人所得成等差數列,且使較大的三份之和的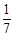 是較小的兩份之和,則最小的
是較小的兩份之和,則最小的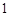 份為
份為
A.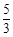 B.
B.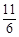 C.
C.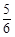 D.
D.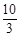
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com