
如下圖已知拋物線y2=2px(p>0)的焦點為F,A是拋物線上橫坐標為4且位于x軸上方的點,A到拋物線準線的距離等于5.過A作AB垂直于y軸,垂足為B,OB的中點為M.
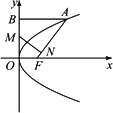
(1)求拋物線方程;
(2)求M作MN⊥FA,垂足為N,求點N的坐標;
(3)以M為圓心,MB為半徑作圓M,當K(m,0)是x軸上一動點時,討論直線AK與圓M的位置關系.
|
解析:(1)拋物線y2=2px的準線為x= (2)∵點A的坐標是(4,4),由題意得B(0,4),M(0,2). 又∵F(1,0), ∴KFA= ∴KMN= 則FA的方程為y= ∴N( (3)由題意得,圓M的圓心是點(0,2),半徑為2,當m=4時,直線AK的方程為x=4,此時,直線AK與圓M相離, 當m≠4時,直線AK的方程為y= 即為4x-(4-m)y-4m=0, 圓心M(0,2)到直線AK的距離d= 解得m>1. ∴當m>1時,直線AK與圓M相離; 當m=1時,直線AK與圓M相切; 當m<1時,直線AK與圓M相交. |


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源:導學大課堂選修數學2-1蘇教版 蘇教版 題型:047
已知點A(2,8),B(x1,y1),C(x2,y2)在拋物線y2=2px上,△ABC的重心與此拋物線的焦點F重合(如下圖).

(1)寫出該拋物線的方程和焦點F的坐標;
(2)求線段BC中點M的坐標.
查看答案和解析>>
科目:高中數學 來源:全優設計選修數學-2-1蘇教版 蘇教版 題型:044
已知點A(2,8),B(x1,y1),C(x2,y2)在拋物線y2=2px上,△ABC的重心與此拋物線的焦點F重合(如下圖).
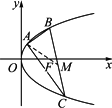
(1)寫出該拋物線的方程和焦點F的坐標;
(2)求線段BC中點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com