【題目】已知x，y滿足不等式組 
，求
（1）z=x+2y的最大值；
（2）z=x2+y2﹣10y+25的最小值．
【答案】
（1）解：由約束條件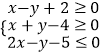 
表示的可行域如下圖所示，
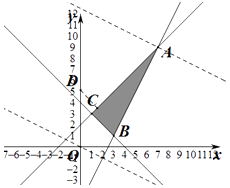
由z=x+2y，得y=﹣ 
，
平移直線y=﹣ ，由圖象可知當直線y=﹣ 經過點A時，直線y=﹣ 的截距最大，此時z最大，
由 
得 
，即A（7，9），此時z=7+2×9=25
（2）解：z=x2+y2﹣10y+25=x2+（y﹣5）2，z的幾何意義為點P（x，y）到點（0，5）的距離的平方；
由圖知，最小值為（0，5）到直線x﹣y+2=0的距離的平方，
即d2=（ 
）2= 
．經檢驗，垂足在線段AC上
【解析】（1）作出不等式組對應的平面區域，利用直線平行進行求解即可．（2）z的幾何意義是兩點間的距離的平方，利用點到直線的距離公式進行求解即可．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）=ax2+2x+c的對稱軸為x=1，g（x）=x+ 
（x＞0）．
（1）求函數g（x）的最小值及取得最小值時x的值；
（2）試確定c的取值范圍，使g（x）﹣f（x）=0至少有一個實根；
（3）若F（x）=﹣f（x）+4x+c，存在實數t，對任意x∈[1，m]，使F（x+t）≤3x恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“累積凈化量
”是空氣凈化器質量的一個重要衡量指標，它是指空氣凈化從開始使用到凈化效率為50%時對顆粒物的累積凈化量，以克表示，根據
《空氣凈化器》國家標準，對空氣凈化器的累計凈化量有如下等級劃分：
累積凈化量（克） |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器（共5000臺）的質量，隨機抽取
臺機器作為樣本進行估計，已知這臺機器的累積凈化量都分布在區間
中，按照
、
、
、
、
均勻分組，其中累積凈化量在的所有數據有：4.5,4.6,5.2,5.3,5.7和5.9，并繪制了頻率分布直方圖，如圖所示：
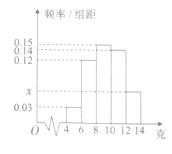
（1）求的值及頻率分布直方圖中
的值；
（2）以樣本估計總體，試估計這批空氣凈化器（共5000臺）中等級為
的空氣凈化器有多少臺？
（3）從累積凈化量在的樣本中隨機抽取2臺，求恰好有1臺等級為的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經過原點的直線與橢圓
交于
兩點，點
為橢圓上不同于
的一點，直線
的斜率均存在，且直線
的斜率之積為
.
（1）求橢圓
的離心率；
（2）設
分別為橢圓的左、右焦點，斜率為
的直線
經過橢圓的右焦點，且與橢圓交于
兩點.若點
在以
為直徑的圓內部，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，以坐標原點為極點， 
軸正半軸為極軸建立極坐標系，圓
的極坐標方程為
，圓
的極坐標方程為
，已知
與
交于
、
兩點，點
位于第一象限．
（Ⅰ）求點
和點
的極坐標；
（Ⅱ）設圓
的圓心為
，點
是直線
上的動點，且滿足
，若直線
的參數方程為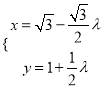
（
為參數），則
的值為多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下結論正確的是（ ）
A.若a＜b且c＜d，則ac＜bd
B.若ac2＞bc2 ， 則a＞b
C.若a＞b，c＜d，則a﹣c＜b﹣d
D.若0＜a＜b，集合A={x|x= 
}，B={x|x= 
}，則A?B
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知左焦點為F（﹣1，0）的橢圓過點E（1， 
）．過點P（1，1）分別作斜率為k1 ， k2的橢圓的動弦AB，CD，設M，N分別為線段AB，CD的中點．
（1）求橢圓的標準方程；
（2）若P為線段AB的中點，求k1；
（3）若k1+k2=1，求證直線MN恒過定點，并求出定點坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
