已知函數f(x)=x2(x-a),其中a∈R.g(x)=f(x)+f'(x).
(I)當函數f(x)的圖象在點(1,f(1))處的切線斜率為2時,求此直線在y軸上的截距;
(II)求證:g(x)既有極大值又有極小值;
(III)若g(x)取極大值和極小值對應的x值分別在區間(-2,-1)和(3,4)內,求實數a的取值范圍.
【答案】
分析:(I)求出f(x)的導函數,求出f'(1)=3-2a,令其為2求出a的值,寫出切線的方程,令方程中的x=0得到直線在y軸上的截距.
(II)求出g′(x)=3x
2-2ax+6x-2a,得到其判別式大于0恒成立,即證得g(x)既有極大值又有極小值
(III)根據題意得到g′(x)=3x
2-2ax+6x-2a的根的分布情況,結合二次函數圖象列出不等式,求出a的范圍.
解答:解:(I)f(x)=x
2(x-a)=x
3-ax
2
f'(x)=3x
2-2ax,
所以所以3-2a=2得

所以f(1)=

所以切線的方程為4x-2y-3=0
令x=0得
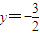
所以此直線在y軸上的截距為
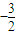
.
(II)因為g(x))=x
3-ax
2+3x
2-2ax
所以g′(x)=3x
2-2ax+6x-2a
△=4a
2+36>0
所以g′(x)=3x
2-2ax+6x-2a有兩個不等根,
所以g(x)既有極大值又有極小值;
(III)因為g(x)取極大值和極小值對應的x值分別在區間(-2,-1)和(3,4)內,
所以
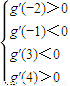
即

解之得
 點評:
點評:解決函數的性質問題,常借助導數,利用導數求曲線的切線時,一定注意函數在切點處的導數值為曲線的切線的斜率.



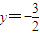
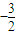 .
.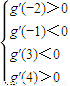 即
即



 閱讀快車系列答案
閱讀快車系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<