
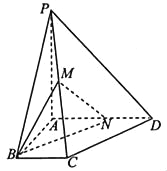
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M為PC的中點點N在線段AD上.
(1)點N為線段AD的中點時,求證:直線PA∥面BMN;
(2)若直線MN與平面PBC所成角的正弦值為![]() ,求二面角C﹣BM﹣N所成角θ的余弦值.
,求二面角C﹣BM﹣N所成角θ的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)連結點![]() ,
,![]() ,交于點
,交于點![]() ,連結
,連結![]() ,推導出四邊形
,推導出四邊形![]() 為正方形,由此能證明直線
為正方形,由此能證明直線![]() 平面
平面![]() ;(2)分別以
;(2)分別以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,由此能求出二面角C-BM-N所成角
軸,建立空間直角坐標系,由此能求出二面角C-BM-N所成角![]() 的余弦值.
的余弦值.
證明:(1)連結點AC,BN,交于點E,連結ME,
∵點N為線段AD的中點,AD=4,
∴AN=2,∵∠ABC=∠BAD=90°,AB=BC=2,
∴四邊形ABCN為正方形,∴E為AC的中點,
∴ME∥PA,
∵PA平面BMN,∴直線PA∥平面BMN.
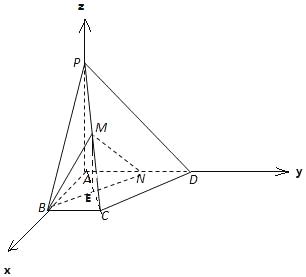
(2)∵PA⊥平面ABCD,且AB,AD平面ABCD,
∴PA⊥AB,PA⊥AD,
∵∠BAD=90°,∴PA,AB,AD兩兩互相垂直,
分別以AB,AD,AP為x,y,z軸,建立空間直角坐標系,
則由AD=AP=4,AB=BC=2,得:
B(2,0,0),C(2,2,0),P(0,0,4),
∵M為PC的中點,∴M(1,1,2),
設AN=λ,則N(0,λ,0),(0≤λ≤4),則![]() =(﹣1,λ﹣1,﹣2),
=(﹣1,λ﹣1,﹣2),
![]() =(0,2,0),
=(0,2,0),![]() =(2,0,﹣4),
=(2,0,﹣4),
設平面PBC的法向量為![]() =(x,y,z),
=(x,y,z),

![]()
∵直線MN與平面PBC所成角的正弦值為![]() ,
,![]() =
=![]() =
=![]() .
.
解得λ=1,則N(0,1,0),![]() =(﹣2,1,0),
=(﹣2,1,0),![]() =(﹣1,1,2),
=(﹣1,1,2),
設平面BMN的法向量![]() =(x,y,z),
=(x,y,z),
![]() =﹣x+y+2z=0,
=﹣x+y+2z=0,![]() =﹣2x+y=0,
=﹣2x+y=0,
令x=2,得![]() =(2,4,﹣1),
=(2,4,﹣1),
cos![]() =
=![]()
∴二面角C-BM-N所成角![]() 的余弦值為
的余弦值為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知圓O經過橢圓C:![]() =1(a>b>0)的兩個焦點以及兩個頂點,且點(b,
=1(a>b>0)的兩個焦點以及兩個頂點,且點(b,![]() )在橢圓C上.
)在橢圓C上.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若直線l與圓O相切,與橢圓C交于M、N兩點,且|MN|=![]() ,求直線l的傾斜角.
,求直線l的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,兩焦點分別為雙曲線
的中心在坐標原點,兩焦點分別為雙曲線![]() 的頂點,直線
的頂點,直線![]() 與橢圓
與橢圓![]() 交于A,B兩點,且點A的坐標為
交于A,B兩點,且點A的坐標為![]() ,點Р是橢圓
,點Р是橢圓![]() 上異于A,B的任意一點,點Q滿足
上異于A,B的任意一點,點Q滿足![]() ,
,![]() ,且A,B,Q三點不共線.
,且A,B,Q三點不共線.
(1)求橢圓![]() 的方程;
的方程;
(2)求點Q的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了![]() 至
至![]() 月份每月
月份每月![]() 號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日期 |
|
|
|
|
|
|
晝夜溫差 |
|
|
|
|
|
|
就診人數 |
|
|
|
| 16 |
|
該興趣小組確定的研究方案是:先從這六組數據中選取![]() 組,用剩下的
組,用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1)求選取的2組數據恰好是相鄰兩個月的概率;
(2)若選取的是![]() 月與
月與![]() 月的兩組數據,請根據
月的兩組數據,請根據![]() 至
至![]() 月份的數據,求出
月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過![]() 人,則認為得到的線性回歸方程是理想的,試問(2)中所得線性回歸方程是否理想?
人,則認為得到的線性回歸方程是理想的,試問(2)中所得線性回歸方程是否理想?
參考公式:
img src="http://thumb.zyjl.cn/questionBank/Upload/2018/08/07/18/7f4fe67a/SYS201808071848019525920497_ST/SYS201808071848019525920497_ST.020.png" width="244" height="61" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A,B分別為雙曲線![]() (a>0,b>0)的左、右頂點,雙曲線的實軸長為4
(a>0,b>0)的左、右頂點,雙曲線的實軸長為4![]() ,焦點到漸近線的距離為
,焦點到漸近線的距離為![]() .
.
(1)求雙曲線的方程;
(2)已知直線y=![]() x-2與雙曲線的右支交于M,N兩點,且在雙曲線的右支上存在點D,使
x-2與雙曲線的右支交于M,N兩點,且在雙曲線的右支上存在點D,使![]() ,求t的值及點D的坐標.
,求t的值及點D的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com