
【題目】已知![]() 是函數
是函數![]() 的導函數,且
的導函數,且![]() ,
,![]() ,則下列說法正確的是___________.
,則下列說法正確的是___________.
①![]() ;
;
②曲線![]() 在
在![]() 處的切線斜率最小;
處的切線斜率最小;
③函數![]() 在
在![]() 存在極大值和極小值;
存在極大值和極小值;
④![]() 在區間
在區間![]() 上至少有一個零點.
上至少有一個零點.
【答案】②③④
【解析】
根據![]() 的導數
的導數![]() 的正負性來判斷
的正負性來判斷![]() 的單調性,逐個選項進行判斷.
的單調性,逐個選項進行判斷.
因為![]() ,所以
,所以![]() ,那么
,那么![]() ,即
,即![]() ,又因為
,又因為![]() ,所以
,所以![]() ,
,![]() .①中
.①中![]() 不能從條件判斷出來,比如
不能從條件判斷出來,比如![]() 和
和![]() 均符合題中函數,但是
均符合題中函數,但是![]() 可正可負.,所以①錯誤。②曲線
可正可負.,所以①錯誤。②曲線![]() 的曲線切線斜率最小即
的曲線切線斜率最小即![]() 的函數值最小,又由
的函數值最小,又由![]() 知道二次函數
知道二次函數![]() 的開口朝上,所以
的開口朝上,所以![]() 在對稱軸即
在對稱軸即![]() 的值最小,所以②正確.
的值最小,所以②正確.
③函數![]() 在
在![]() 是否存在極大值和極小值取決于
是否存在極大值和極小值取決于![]() 的正負性,而
的正負性,而![]() 是開口朝上的二次函數,又因為
是開口朝上的二次函數,又因為![]() ,所以
,所以![]() 存在
存在![]() 兩個零點,并且在
兩個零點,并且在![]() 上
上![]() ,在
,在![]() 上
上![]() ,在
,在![]() 上
上![]() .可知
.可知![]() 在
在![]() 取得極大值,在
取得極大值,在![]() 取得極小值,所以③正確。④
取得極小值,所以③正確。④![]() ,而
,而![]() ,
,
![]() ,所以
,所以![]() ,那么
,那么![]() 之間至少有一個數為正,而
之間至少有一個數為正,而![]() 因為
因為![]() 的圖像是一條連續的曲線,所以若
的圖像是一條連續的曲線,所以若![]() ,
,![]() 可得在
可得在![]() 在
在![]() 至少有一個零點,若
至少有一個零點,若![]() ,
,![]() 可得在
可得在![]() 在
在![]() 至少有一個零點,所以
至少有一個零點,所以![]() 在區間
在區間![]() 上至少有一個零點. ④正確。所以此題①錯誤,②③④正確。
上至少有一個零點. ④正確。所以此題①錯誤,②③④正確。


科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.若![]() 為真命題,則
為真命題,則![]() ,
,![]() 均為假命題;
均為假命題;
B.命題“若![]() ,則
,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
C.等比數列![]() 的前
的前![]() 項和為
項和為![]() ,若“
,若“![]() ”則“
”則“![]() ”的否命題為真命題;
”的否命題為真命題;
D.“平面向量![]() 與
與![]() 的夾角為鈍角”的充要條件是“
的夾角為鈍角”的充要條件是“![]() ”
”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,且曲線
,且曲線![]() 與
與![]() 恰有一個公共點.
恰有一個公共點.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)已知曲線![]() 上兩點
上兩點![]() ,
,![]() 滿足
滿足![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,設橢圓
中,設橢圓![]() 的左焦點為
的左焦點為![]() ,短軸的兩個端點分別為
,短軸的兩個端點分別為![]() ,且
,且![]() ,點
,點![]() 在
在![]() 上.
上.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若直線![]() 與橢圓
與橢圓![]() 和圓
和圓![]() 分別相切于
分別相切于![]() ,
,![]() 兩點,當
兩點,當![]() 面積取得最大值時,求直線
面積取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,《宋人撲棗圖軸》是作于宋朝的中國古畫,現收藏于中國臺北故宮博物院.該作品簡介:院角的棗樹結實累累,小孩群來攀扯,枝椏不停晃動,粒粒棗子搖落滿地,有的牽起衣角,有的捧著盤子拾取,又玩又吃,一片興高采烈之情,躍然于絹素之上.甲、乙、丙、丁四人想根據該圖編排一個舞蹈,舞蹈中他們要模仿該圖中小孩撲棗的爬、扶、撿、頂四個動作,四人每人模仿一個動作.若他們采用抽簽的方式來決定誰模仿哪個動作,則甲不模仿“爬”且乙不模仿“扶”的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國上是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照
的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照![]() ,
, ![]() ,…,
,…, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)已知該市有80萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使![]() 的居民每月的用水量不超過標準
的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由;
的值,并說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量結果得如下頻率分布直方圖:
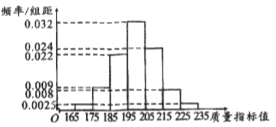
(1)求這100件產品質量指標值的樣本平均數![]() 和樣本方差
和樣本方差![]() (同一組的數據用該組區間的中點值作為代表);
(同一組的數據用該組區間的中點值作為代表);
(2)由直方圖可以認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() 。
。
(i)若某用戶從該企業購買了10件這種產品,記![]() 表示這10件產品中質量指標值位于(187.4,225.2)的產品件數,求
表示這10件產品中質量指標值位于(187.4,225.2)的產品件數,求![]() ;
;
(ii)一天內抽取的產品中,若出現了質量指標值在![]() 之外的產品,就認為這一天的生產過程中可能出現了異常情況,需對當天的生產過程進行檢查下。下面的莖葉圖是檢驗員在一天內抽取的15個產品的質量指標值,根據近似值判斷是否需要對當天的生產過程進行檢查。
之外的產品,就認為這一天的生產過程中可能出現了異常情況,需對當天的生產過程進行檢查下。下面的莖葉圖是檢驗員在一天內抽取的15個產品的質量指標值,根據近似值判斷是否需要對當天的生產過程進行檢查。

附:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com