
已知函數(shù) (
( ),其圖像在點(diǎn)(1,
),其圖像在點(diǎn)(1, )處的切線方程為
)處的切線方程為 .
.
(1)求 ,
, 的值;
的值;
(2)求函數(shù) 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(3)求函數(shù) 在區(qū)間[-2,5]上的最大值.
在區(qū)間[-2,5]上的最大值.
(1) 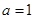 ,
,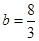 .
.
(2)函數(shù) 的極大值是
的極大值是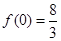 ,極小值是
,極小值是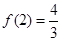 .
.
(3)函數(shù) 在區(qū)間
在區(qū)間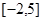 上的最大值為
上的最大值為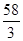 .
.
【解析】
試題分析:(1) 由題意,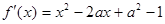 .
1分
.
1分
又∵函數(shù) 的圖象在點(diǎn)
的圖象在點(diǎn)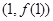 處的切線方程為
處的切線方程為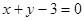 ,
,
所以切線的斜率為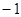 ,
,
即 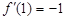 ,∴
,∴ ,解得
,解得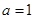 .
2分
.
2分
又∵點(diǎn)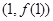 在直線
在直線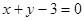 上,∴
上,∴ , 3分
, 3分
同時(shí)點(diǎn)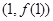 即點(diǎn)
即點(diǎn)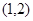 在
在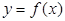 上,
上,
∴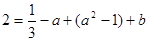 , 4分
, 4分
即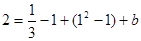 ,解得
,解得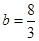 . 5分
. 5分
(2)由(1)有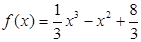 ,
,
∴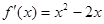 ,
6分
,
6分
由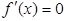 可知
可知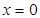 ,或
,或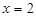 ,所以有
,所以有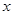 、
、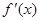 、
、 的變化情況表如下:
的變化情況表如下:
|
|
|
|
|
|
|
|
|
+ |
|
- |
|
+ |
|
|
|
極大值 |
|
極小值 |
|
8分
由上表可知, 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是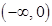 和
和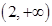 ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是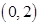 ; 10分
; 10分
∴函數(shù) 的極大值是
的極大值是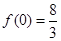 ,極小值是
,極小值是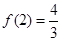 .
11分
.
11分
(3)由(2),函數(shù) 在區(qū)間
在區(qū)間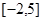 上的極大值是
上的極大值是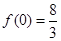 .
12分
.
12分
又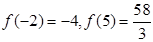 ,
13分
,
13分
∴函數(shù) 在區(qū)間
在區(qū)間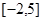 上的最大值為
上的最大值為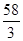 . 14分
. 14分
考點(diǎn):導(dǎo)數(shù)的幾何意義,應(yīng)用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、極(最值)值。
點(diǎn)評(píng):典型題,本題屬于導(dǎo)數(shù)內(nèi)容中的基本問題,(1)運(yùn)用“函數(shù)在某點(diǎn)的切線斜率,就是該點(diǎn)的導(dǎo)數(shù)值”,確定直線的斜率。通過研究導(dǎo)數(shù)值的正負(fù)情況,明確函數(shù)的單調(diào)區(qū)間。確定函數(shù)的最值,往往遵循“求導(dǎo)數(shù),求駐點(diǎn),計(jì)算極值、端點(diǎn)函數(shù)值,比較大小確定最值”。


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2010-2011年浙江省溫州市蒼南中學(xué)高二下學(xué)期期末考試文數(shù) 題型:單選題
已知函數(shù)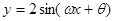 為偶函數(shù)
為偶函數(shù)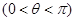 ,其圖像與直線
,其圖像與直線 的某兩個(gè)交點(diǎn)的橫坐標(biāo)為
的某兩個(gè)交點(diǎn)的橫坐標(biāo)為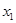 ,
,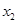 ,若
,若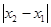 的最小值為
的最小值為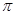 ,則( )
,則( )
A.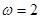 , ,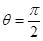 | B.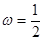 , ,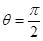 |
C.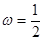 , ,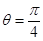 | D.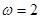 , ,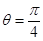 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014屆重慶南開中學(xué)高三上學(xué)期9月月考理科數(shù)學(xué)試卷(解析版) 題型:選擇題
已知函數(shù)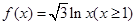 ,若將其圖像繞原點(diǎn)逆時(shí)針旋轉(zhuǎn)
,若將其圖像繞原點(diǎn)逆時(shí)針旋轉(zhuǎn) 角后,所得圖像仍是某函數(shù)的圖像,則當(dāng)角
角后,所得圖像仍是某函數(shù)的圖像,則當(dāng)角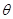 取最大值
取最大值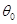 時(shí),
時(shí),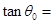 ( )
( )
A. B.
B.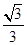 C.
C.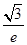 D.
D.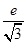
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012年人教B版高中數(shù)學(xué)必修一2.1函數(shù)奇偶性練習(xí)卷(四)(解析版) 題型:選擇題
已知函數(shù) 是偶函數(shù),其圖像與x軸有四個(gè)交點(diǎn),則方程
是偶函數(shù),其圖像與x軸有四個(gè)交點(diǎn),則方程 的所有實(shí)數(shù)根的和為( )
的所有實(shí)數(shù)根的和為( )
A.4 B.2 C.1 D.0
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年浙江省溫州市高二下學(xué)期期末考試文數(shù) 題型:選擇題
已知函數(shù) 為偶函數(shù)
為偶函數(shù)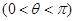 ,其圖像與直線
,其圖像與直線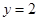 的某兩個(gè)交點(diǎn)的橫坐標(biāo)為
的某兩個(gè)交點(diǎn)的橫坐標(biāo)為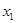 ,
,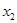 ,若
,若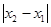 的最小值為
的最小值為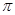 ,則( )
,則( )
A.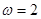 ,
,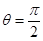 B.
B.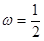 ,
,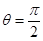
C.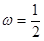 ,
,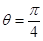 D.
D.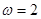 ,
,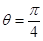
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com