
【題目】已知數列{an}滿足a1=9,an+1=an+2n+5;數列{bn}滿足b1= ![]() ,bn+1=
,bn+1= ![]() bn(n≥1).
bn(n≥1).
(1)求an , bn;
(2)記數列{ ![]() }的前n項和為Sn , 證明:
}的前n項和為Sn , 證明: ![]() ≤Sn<
≤Sn< ![]() .
.
【答案】
(1)解:由an+1=an+2n+5得an+1﹣an=2n+5,
則a2﹣a1=7,
a3﹣a2=9,
…
an﹣1﹣an﹣2=2(n﹣2)+5,
an﹣an﹣1=2(n﹣1)+5=2n+3
等式兩邊同時相加得
an﹣a1= ![]() ×(n﹣1)=(5+n)(n﹣1)=n2+4n﹣5,
×(n﹣1)=(5+n)(n﹣1)=n2+4n﹣5,
則an=a1+n2+4n﹣5=n2+4n﹣5+9=n2+4n+4,
所以數列{an}的通項公式為 ![]() .
.
又∵ ![]() ,
, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
,
將上述(n﹣1)個式子相乘,得 ![]() ,即
,即 ![]() .
.
(2)解:∵ ![]() .
.
∵ ![]() =
= ![]() ,
,
![]() ,∴
,∴ ![]()
【解析】(1)利用數列的遞推關系,利用累加法和累積法進行求解即可.(2)求出數列{ ![]() }的通項公式,利用裂項法進行求解,結合不等式的性質進行證明即可.
}的通項公式,利用裂項法進行求解,結合不等式的性質進行證明即可.
【考點精析】根據題目的已知條件,利用數列的前n項和和數列的通項公式的相關知識可以得到問題的答案,需要掌握數列{an}的前n項和sn與通項an的關系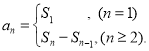 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式.


科目:高中數學 來源: 題型:
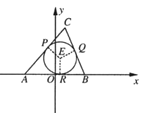
【題目】已知△ABC的兩頂點坐標A(﹣1,0),B(1,0),圓E是△ABC的內切圓,在邊AC,BC,AB上的切點分別為P,Q,R,|CP|=1(從圓外一點到圓的兩條切線段長相等),動點C的軌跡為曲線M.
(I)求曲線M的方程;
(Ⅱ)設直線BC與曲線M的另一交點為D,當點A在以線段CD為直徑的圓上時,求直線BC的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點.
上的點.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中點,且二面角
的中點,且二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}為等比數列,a1=1,a6=243.Sn為等差數列{bn}的前n項和,b1=1,S5=25.
(1)求{an}和{bn}的通項公式;
(2)設Tn=a1b1+a2b2+…+anbn , 求Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的不等式mx2+2x+6m>0,在下列條件下分別求m的值或取值范圍:
(1)不等式的解集為{x|2<x<3};
(2)不等式的解集為R.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}中,已知a1=2,a4=16.
(1)求數列{an}的通項公式an;
(2)若a3 , a5分別是等差數列{bn}的第4項和第16項,求數列{bn}的通項公式及前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com