Question

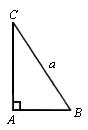
如圖，在RtDABC中，已知BC=a，若長為2a的線段PQ以點A為中點，問與的夾角q取何值時的值最大?并求出這個最大值．

Answer 1

答案：
解析：

本小題主要考查向量的概念，平面向量的運算法則，考查運用向量及函數知識的能力． 解法一：∵ ，∴ ∵ ∴ =-a2+a2cosq． 故當cosq=1時，即q=0（與方向相同）時，最大，其最大值為0． 解法二：以直角頂點A為坐標原點，兩直角邊所在直線為坐標軸建立如圖所示的平面直角坐標系． 設=c，=b，則A(0，0)，B(c，0)，C(0，b)，且=2a，=a 設點P的坐標為(x，y)，則Q(-x，-y)． ∴ =(x-c，y)，=(-x，-y-b)， =(-c，b)，=(-2x，-2y)． ∴ =(x-c)(-x)+y(-y-b)=-(x2+y2)+cx-by． ∵ ∴ cx-by=a2cosq ∴ =-a2+a2cosq 故當cosq=1時，即q=0（與方向相同）時，最大，其最大值為0．