
【題目】已知![]() ,
,![]() .
.
(1)當![]() 時,求證:
時,求證:![]() ;
;
(2)若存在![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)見證明;(2)![]()
【解析】
(1) 設F(x)=e2x+ln(x+1)﹣(x+1)2﹣x(x≥0),通過兩次求導,判斷F(x)的單調性,即可得證;(2) 由題意可得存在x0∈[0,+∞),使得e![]() ﹣ln(x0+a)﹣x02<0,設
﹣ln(x0+a)﹣x02<0,設![]() =e2x﹣ln(x+a)﹣x2,兩次求導,判斷單調性,對a討論,分①當a≥
=e2x﹣ln(x+a)﹣x2,兩次求導,判斷單調性,對a討論,分①當a≥![]() 時,②當a<
時,②當a<![]() 時,通過構造函數和求導,得到單調區間,可得最值,即可得到所求a的范圍.
時,通過構造函數和求導,得到單調區間,可得最值,即可得到所求a的范圍.
(1)設![]() ,
,![]()
F″(x)=4e2x﹣![]() ﹣2=[e2x-
﹣2=[e2x-![]() ]+2(e2x﹣1)+e2x>0,(x≥0),
]+2(e2x﹣1)+e2x>0,(x≥0),
所以,F′(x)在[0,+∞)上遞增,所以F′(x)≥F′(0)=0,
所以,F(x)在[0,+∞)上遞增,所以F(x)≥F(0)=0,
即有當x≥0時,f(x)≥(x+1)2+x;
(2)即![]() ,
,
則![]() ,
,![]()
![]() 在
在![]() 上遞增,
上遞增,![]()
①當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為單調遞增函數,
上為單調遞增函數,
故![]() ,
,![]()
②當![]() 時,
時,![]()
設![]() ,
,
![]() ,
,
![]() 在
在![]() 上為單調遞增函數,
上為單調遞增函數,
![]() ,
,
![]() ,
,
則當![]() 時,
時,![]() 恒成立,不合題意
恒成立,不合題意
綜上,則![]()


科目:高中數學 來源: 題型:
【題目】PM2.5是指空氣中直徑小于或等于2.5微米的顆粒物(也稱可入肺顆粒物).為了探究車流量與PM2.5的濃度是否相關,現采集到某城市周一至周五某一時間段車流量與PM2.5的數據如下表:
時間 | 周一 | 周二 | 周三 | 周四 | 周五 |
車流量×(萬輛) | 50 | 51 | 54 | 57 | 58 |
PM2.5的濃度(微克/立方米) | 60 | 70 | 74 | 78 | 79 |
(1)根據上表數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(2)若周六同一時間段的車流量是25萬輛,試根據(1)求出的線性回歸方程,預測此時PM2.5的濃度為多少(保留整數)?
參考公式:由最小二乘法所得回歸直線的方程是:![]() ,其中
,其中 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
11分制乒乓球比賽,每贏一球得1分,當某局打成10:10平后,每球交換發球權,先多得2分的一方獲勝,該局比賽結束.甲、乙兩位同學進行單打比賽,假設甲發球時甲得分的概率為0.5,乙發球時甲得分的概率為0.4,各球的結果相互獨立.在某局雙方10:10平后,甲先發球,兩人又打了X個球該局比賽結束.
(1)求P(X=2);
(2)求事件“X=4且甲獲勝”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解甲、乙兩種離子在小鼠體內的殘留程度,進行如下試驗將![]() 只小鼠隨機分成
只小鼠隨機分成![]() 、
、![]() 兩組,每組
兩組,每組![]() 只,其中
只,其中![]() 組小鼠給服甲離子溶液,
組小鼠給服甲離子溶液,![]() 組小鼠給服乙離子溶液每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比根據試驗數據分別得到如圖所示的直方圖:
組小鼠給服乙離子溶液每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內離子的百分比根據試驗數據分別得到如圖所示的直方圖:


根據頻率分布直方圖估計,事件![]() :“乙離子殘留在體內的百分比不高于
:“乙離子殘留在體內的百分比不高于![]() ”發生的概率
”發生的概率![]() .
.
(1)根據所給的頻率分布直方圖估計各段頻數;
(附:頻數分布表)
|
|
|
|
|
|
| |
|
|
| |
|
|
|
|
|
|
| |
|
|
| |
(2)請估計甲離子殘留百分比的中位數,請估計乙離子殘留百分比的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校隨機抽取部分新生調查其上學所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖),其中上學所需時間的范圍是![]() ,樣本數據分組為
,樣本數據分組為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方圖中x的值;
(2)如果上學所需時間不少于1小時的學生可申請在學校住宿,若該學校有600名新生,請估計新生中有多少名學生可以申請住宿;
(3)由頻率分布直方圖估計該校新生上學所需時間的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解中學生對交通安全知識的掌握情況,從農村中學和城鎮中學各選取100名同學進行交通安全知識競賽.下圖1和圖2分別是對農村中學和城鎮中學參加競賽的學生成績按![]() ,
,![]() ,
,![]() ,
,![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.
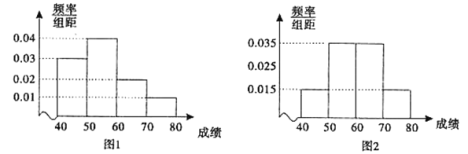
(Ⅰ)分別估算參加這次知識競賽的農村中學和城鎮中學的平均成績;
(Ⅱ)完成下面![]() 列聯表,并回答是否有
列聯表,并回答是否有![]() 的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
的把握認為“農村中學和城鎮中學的學生對交通安全知識的掌握情況有顯著差異”?
成績小于60分人數 | 成績不小于60分人數 | 合計 | |
農村中學 | |||
城鎮中學 | |||
合計 |
附:![]()
臨界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數AQI是反映空氣質量狀況的指數,AQI指數值越小,表明空氣質量越好,其對應關系如下表:
AQI指數值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數變化趨勢:

下列敘述錯誤的是
A. 這20天中AQI指數值的中位數略高于100
B. 這20天中的中度污染及以上的天數占![]()
C. 該市10月的前半個月的空氣質量越來越好
D. 總體來說,該市10月上旬的空氣質量比中旬的空氣質量好
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com