
分析 (1)求出f′(x),令f′(x)小于0求出x的范圍即為函數的減區間,令f′(x)大于0求出x的范圍即為函數的增區間;
(2)當0<t<t+2<$\frac{1}{e}$時t無解,當0<t≤$\frac{1}{e}$<t+2即0<t≤$\frac{1}{e}$時,根據函數的增減性得到f(x)的最小值為f($\frac{1}{e}$),當$\frac{1}{e}$<t<t+2即t>$\frac{1}{e}$時,函數為增函數,得到f(x)的最小值為f(t);
(3)求出g′(x),把f(x)和g′(x)代入2f(x)≤g′(x)+2中,根據x大于0解出a≥lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,然后令h(x)=lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,求出h(x)的最大值,a大于等于h(x)的最大值,方法是先求出h′(x)=0時x的值,利用函數的定義域和x的值分區間討論導函數的正負得到函數的單調區間,根據函數的增減性即可得到函數的最大值,即可求出a的取值范圍.
解答 解:(1)f′(x)=lnx+1令f′(x)<0解得0<x<$\frac{1}{e}$,
∴f(x)的單調遞減區間為(0,$\frac{1}{e}$)
令f′(x)>0解得x>$\frac{1}{e}$,
∴f(x)的單調遞增區間為($\frac{1}{e}$,+∞);
(2)當0<t<t+2<$\frac{1}{e}$時,t無解
當0<t≤$\frac{1}{e}$<t+2,即0<t≤$\frac{1}{e}$時,
∴f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$;
當$\frac{1}{e}$<t<t+2,即t>$\frac{1}{e}$時,f(x)在[t,t+2]上單調遞增,
∴f(x)min=f(t)=tlnt
∴f(x)min=$\left\{\begin{array}{l}{-\frac{1}{e},0<t≤\frac{1}{e}}\\{tlnt,t>\frac{1}{e}}\end{array}\right.$;
(3)由題意:2xlnx≤3x2+2ax-1+2即2xlnx≤3x2+2ax+1
∵x∈(0,+∞)
∴a≥lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,
設h(x)=lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,
則h′(x)=$\frac{1}{x}$-$\frac{3}{2}$+$\frac{1}{{2x}^{2}}$=-$\frac{(x-1)(3x+1)}{{2x}^{2}}$,
令h′(x)=0,得x=1,x=-$\frac{1}{3}$(舍)
當0<x<1時,h′(x)>0;當x>1時,h′(x)<0
∴當x=1時,h(x)取得最大值,h(x)max=-2
∴a≥-2
故實數a的取值范圍[-2,+∞).
點評 本題要求學生會利用導函數的正負得到函數的額單調區間以及會根據函數的增減性得到函數的極值,掌握不等式恒成立時所滿足的條件,是一道中檔題.


 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
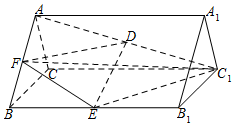 如圖,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分別為AC1和BB1的中點.
如圖,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分別為AC1和BB1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 兩解 | B. | 一解 | C. | 無解 | D. | 無窮多解 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 9 | D. | -9 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com