【答案】
分析:(1)根據題中等式配方得x+y=5+

(
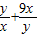
),利用基本不等式求出當且僅當x=2、y=6時
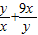
的最小值為6,由此即可得到x+y的最小值;
(2)利用基本不等式,得1=
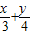
≥2

,平方化簡即可得到當且僅當x=

,y=2時,xy的最大值為

;
(3)原不等式化簡為(1-x)+
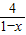
≥2-a,結合1-x>0利用基本不等式求出(1-x)+
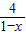
的最小值為4.由此討論不等式
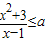
恒成立,可得4≥2-a,即可求出a的取值范圍.
解答:解:(1)由題意得:x+y=

(x+y)(
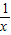
+
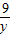
)=5+

(

)
∵
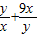
≥2

=6------------------(3分)
∴x+y=5+

(

)≥5+

=8,當且僅當x=2,y=6時等號成立
即x+y的最小值是8--------------------------(4分)
(2)因為x、y為正數,所以1=
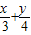
≥2
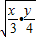
=2
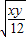
所以
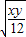
≤

,平方得xy
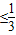
-------------------------------(7分)
∴當且僅當x=

,y=2時,xy的最大值為

-------------------------(8分)
(3)不等式
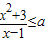
,即
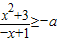
整理,得(1-x)+
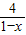
≥2-a
∵x<1,得1-x>0為正數
∴(1-x)+
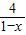
≥2
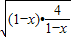
=4
即當且僅當1-x=2,即x=-1時,(1-x)+
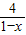
的最小值為4
因此若對任意x<1,
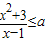
恒成立,即4≥2-a,解之得a≥-2
所以a的取值范圍為[-2,+∞)-----------------------------(12分)
點評:本題給出幾個等式,求相應的最值,并討論不等式恒成立.著重考查了基本不等式求最值、不等式恒成立的討論等知識,屬于中檔題.

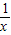 +
+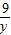 =2,求x+y的最小值.
=2,求x+y的最小值.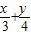 =1,求xy的最大值.
=1,求xy的最大值.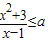 恒成立,求a的取值范圍.
恒成立,求a的取值范圍. (
(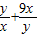 ),利用基本不等式求出當且僅當x=2、y=6時
),利用基本不等式求出當且僅當x=2、y=6時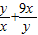 的最小值為6,由此即可得到x+y的最小值;
的最小值為6,由此即可得到x+y的最小值;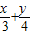 ≥2
≥2 ,平方化簡即可得到當且僅當x=
,平方化簡即可得到當且僅當x= ,y=2時,xy的最大值為
,y=2時,xy的最大值為 ;
;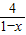 ≥2-a,結合1-x>0利用基本不等式求出(1-x)+
≥2-a,結合1-x>0利用基本不等式求出(1-x)+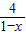 的最小值為4.由此討論不等式
的最小值為4.由此討論不等式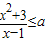 恒成立,可得4≥2-a,即可求出a的取值范圍.
恒成立,可得4≥2-a,即可求出a的取值范圍. (x+y)(
(x+y)(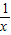 +
+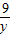 )=5+
)=5+ (
( )
)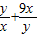 ≥2
≥2 =6------------------(3分)
=6------------------(3分) (
( )≥5+
)≥5+ =8,當且僅當x=2,y=6時等號成立
=8,當且僅當x=2,y=6時等號成立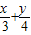 ≥2
≥2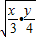 =2
=2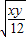
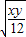 ≤
≤ ,平方得xy
,平方得xy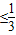 -------------------------------(7分)
-------------------------------(7分) ,y=2時,xy的最大值為
,y=2時,xy的最大值為 -------------------------(8分)
-------------------------(8分)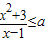 ,即
,即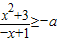
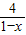 ≥2-a
≥2-a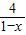 ≥2
≥2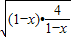 =4
=4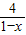 的最小值為4
的最小值為4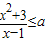 恒成立,即4≥2-a,解之得a≥-2
恒成立,即4≥2-a,解之得a≥-2

 閱讀快車系列答案
閱讀快車系列答案