
【題目】已知函數![]() ,其中a為非零常數.
,其中a為非零常數.
![]() 討論
討論![]() 的極值點個數,并說明理由;
的極值點個數,并說明理由;
![]() 若
若![]() ,
,![]() 證明:
證明:![]() 在區間
在區間![]() 內有且僅有1個零點;
內有且僅有1個零點;![]() 設
設![]() 為
為![]() 的極值點,
的極值點,![]() 為
為![]() 的零點且
的零點且![]() ,求證:
,求證:![]() .
.
【答案】(1)見解析;(2)(i)證明見解析;(ii)證明見解析.
【解析】
![]() 先對函數求導,然后結合導數與單調性的關系,對a進行分類討論即可求解函數的單調性,進而可確定極值,
先對函數求導,然后結合導數與單調性的關系,對a進行分類討論即可求解函數的單調性,進而可確定極值,
![]() 轉化為證明
轉化為證明![]() 只有一個零點,結合函數與導數知識可證;
只有一個零點,結合函數與導數知識可證;
![]() 由題意可得,
由題意可得,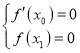 ,代入可得,
,代入可得,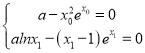 ,結合函數的性質可證.
,結合函數的性質可證.
解:![]() 解:由已知,
解:由已知,![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
①當![]() 時,
時,![]() ,從而
,從而![]() ,
,
所以![]() 在
在![]() 內單調遞減,無極值點;
內單調遞減,無極值點;
②當![]() 時,令
時,令![]() ,
,
則由于![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,
,![]() ,
,
所以存在唯一的![]() ,使得
,使得![]() ,
,
所以當![]() 時,
時,![]() ,即
,即![]() ;當
;當![]() 時,
時,![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 在
在![]() 上有且僅有一個極值點.
上有且僅有一個極值點.
綜上所述,當![]() 時,函數
時,函數![]() 無極值點;當
無極值點;當![]() 時,函數
時,函數![]() 只有一個極值點;
只有一個極值點;
![]() 證明:
證明:![]() 由
由![]() 知
知![]() .
.
令![]() ,由
,由![]() 得
得![]() ,
,
所以![]() 在
在![]() 內有唯一解,從而
內有唯一解,從而![]() 在
在![]() 內有唯一解,
內有唯一解,
不妨設為![]() ,則
,則![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
所以![]() 是
是![]() 的唯一極值點.
的唯一極值點.
令![]() ,則當
,則當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 內單調遞減,
內單調遞減,
從而當![]() 時,
時,![]() ,所以
,所以![]() .
.
從而當![]() 時,
時,![]() ,且
,且![]()
又因為![]() ,故
,故![]() 在
在![]() 內有唯一的零點.
內有唯一的零點.
![]() 由題意,
由題意,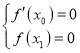 即
即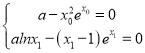 ,
,
從而![]() ,即
,即![]() .
.
因為當![]() 時,
時,![]() ,又
,又![]() ,
,
故![]() ,即
,即![]() ,
,
兩邊取對數,得![]() ,
,
于是![]() ,整理得
,整理得![]() .
.


科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,且過點
,且過點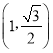 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]()
![]() ,
,![]() 為橢圓
為橢圓![]() 上一點,過點
上一點,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,射線
兩點,射線![]() 交橢圓
交橢圓![]() 于點Q.
于點Q.
(i)若![]() 為橢圓
為橢圓![]() 上任意一點,求
上任意一點,求![]() 的值;
的值;
(ii)若![]() 點坐標為
點坐標為![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分別是棱BC,CD的中點,下面結論正確的是( )
,M,N分別是棱BC,CD的中點,下面結論正確的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱錐A-CMN的體積的最大值為![]() D.AD與BC一定不垂直
D.AD與BC一定不垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術·均輸》中有如下問題:“今有五人分十錢,令上二人所得與下三人等,問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分10錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列,問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,甲所得為( )
A.![]() 錢B.
錢B.![]() 錢C.
錢C.![]() 錢D.
錢D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,點
的左、右焦點,點![]() 關于直線
關于直線![]() 對稱的點Q在橢圓上,則橢圓的離心率為______;若過
對稱的點Q在橢圓上,則橢圓的離心率為______;若過![]() 且斜率為
且斜率為![]() 的直線與橢圓相交于AB兩點,且
的直線與橢圓相交于AB兩點,且![]() ,則
,則![]() ___.
___.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】截至2019年,由新華社《瞭望東方周刊》與瞭望智庫共同主辦的"中國最具幸福感城市"調查推選活動已連續成功舉辦12年,累計推選出60余座幸福城市,全國約9億多人次參與調查,使"城市幸福感"概念深入人心.為了便于對某城市的"城市幸福感"指數進行研究,現從該市抽取若干人進行調查,繪制成如下不完整的2×2列聯表(數據單位:人).
男 | 女 | 總計 | |
非常幸福 | 11 | 15 | |
比較幸福 | 9 | ||
總計 | 30 |
(1)將列聯表補充完整,并據此判斷是否有90%的把握認為城市幸福感指數與性別有關;
(2)若感覺"非常幸福"記2分,"比較幸福"記1分,從上表男性中隨機抽取3人,記3人得分之和為![]() ,求
,求![]() 的分布列,并根據分布列求
的分布列,并根據分布列求![]() 的概率
的概率
附: ,其中
,其中![]() .
.
| 0. 10 | 0. 05 | 0. 010 | 0.001 |
| 2.706 | 3.841 | 6. 635 | 10. 828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,右頂點為A,上頂點為B,且滿足向量
,右頂點為A,上頂點為B,且滿足向量![]() 。
。
(1)若![]() ,求橢圓的標準方程;
,求橢圓的標準方程;
(2)設![]() 為橢圓上異于頂點的點,以線段PB為直徑的圓經過F1,問是否存在過F2的直線與該圓相切?若存在,求出其斜率;若不存在,說明理由。
為橢圓上異于頂點的點,以線段PB為直徑的圓經過F1,問是否存在過F2的直線與該圓相切?若存在,求出其斜率;若不存在,說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com