日韩欧美国产成人一区二区,欧美性久久,91av免费在线

精英家教網 > 高中數學 > 題目詳情

如圖1-4-8，在柱坐標系中，長方體的兩個頂點坐標為A₁(4,0,5),C₁(6,,5)，則此長方體外接球的體積為________________.

圖1-4-8

思路解析：由長方體的兩個頂點坐標為A₁(4,0,5),C₁(6,,5),

可知OA=4,OC=6,OO₁=5,

則對角線長為,

那么球的體積為·π·()³=.

答案：

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

（2008•奉賢區二模）如圖，在正四棱柱ABCD-A₁B₁C₁D₁中，AB=4，AA₁=8．
（1）求異面直線B₁C與A₁C₁所成角的大小；（用反三角函數形式表示）
（2）若E是線段DD₁上（不包含線段的兩端點）的一個動點，請提出一個與三棱錐體積有關的數學問題（注：三棱錐需以點E和已知正四棱柱八個頂點中的三個為頂點構成）；并解答所提出的問題．

查看答案和解析>>

科目：高中數學 來源：2011-2012學年山東省高三第五次質量檢測文科數學試卷（解析版） 題型：解答題

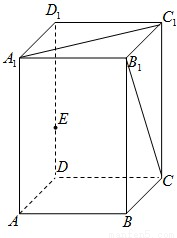
如圖，在正三棱柱ABC-A₁B₁C₁中，底面ABC為正三角形，M、N、G分別是棱CC₁、AB、BC的中點，且.

（Ⅰ）求證：CN∥平面AMB₁；

（Ⅱ）求證： B₁M⊥平面AMG.

【解析】本試題主要是考查了立體幾何匯總線面的位置關系的運用。第一問中，要證CN∥平面AMB₁；，只需要確定一條直線CN∥MP，既可以得到證明

第二問中，∵CC₁⊥平面ABC，∴平面CC₁ B₁ B⊥平面ABC，得到線線垂直，B₁M⊥AG，結合線面垂直的判定定理和性質定理，可以得證。

解：(Ⅰ)設AB₁ 的中點為P，連結NP、MP ………………1分

∵CM ，NP ，∴CM NP， …………2分

∴CNPM是平行四邊形，∴CN∥MP …………………………3分

∵CN 平面AMB₁，MP奐平面AMB₁，∴CN∥平面AMB₁…4分

(Ⅱ)∵CC₁⊥平面ABC，∴平面CC₁ B₁ B⊥平面ABC，

∵AG⊥BC，∴AG⊥平面CC₁ B₁ B，∴B₁M⊥AG………………6分

∵CC₁⊥平面ABC，平面A₁B₁C₁∥平面ABC，∴CC₁⊥AC，CC₁⊥B₁ C，

設：AC=2a，則

…………………………8分

同理，…………………………………9分

∵ BB₁∥CC₁，∴BB₁⊥平面ABC，∴BB₁⊥AB，

………………………………10分

查看答案和解析>>

科目：高中數學 來源：2011-2012學年廣東省肇慶市高三數學復習必修2模塊測試試卷D卷 題型：選擇題

如圖8-25，在三棱柱的側棱A₁A和B₁B上各有一動點P，Q，且滿足A₁P=BQ，過P、Q、C三點的截面把棱柱分成兩部分，則其體積之比為（）

A．3∶1 B．2∶1 C．4∶1 D．∶1

查看答案和解析>>

科目：高中數學 來源：2008年上海市奉賢區高考數學二模試卷（文科）（解析版） 題型：解答題

如圖，在正四棱柱ABCD-A₁B₁C₁D₁中，AB=4，AA₁=8．
（1）求異面直線B₁C與A₁C₁所成角的大小；（用反三角函數形式表示）
（2）若E是線段DD₁上（不包含線段的兩端點）的一個動點，請提出一個與三棱錐體積有關的數學問題（注：三棱錐需以點E和已知正四棱柱八個頂點中的三個為頂點構成）；并解答所提出的問題．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學