
【題目】已知函數![]() 是奇函數.
是奇函數.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)用定義證明函數![]() 在
在![]() 上的單調性;
上的單調性;
(Ⅲ)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)證明見解析;(Ⅲ)
;(Ⅱ)證明見解析;(Ⅲ)![]() .
.
【解析】
試題分析:(Ⅰ)由已知,函數![]() 是
是![]() 上的奇函數,則有
上的奇函數,則有![]() ,從而可解得
,從而可解得![]() ;(Ⅱ)用定義法證明函數單調性的步驟為:①取值,根據定義域(或指定的區域)任取
;(Ⅱ)用定義法證明函數單調性的步驟為:①取值,根據定義域(或指定的區域)任取![]() ,且
,且![]() ;②作差(或作商),
;②作差(或作商),![]() ,對其式子進行化簡整理;③判斷符號,即
,對其式子進行化簡整理;③判斷符號,即![]() ,或
,或![]() ;④下結論;(Ⅲ)由(Ⅰ)、(Ⅱ)可知函數
;④下結論;(Ⅲ)由(Ⅰ)、(Ⅱ)可知函數![]() 是奇函數,且在
是奇函數,且在![]() 上單調遞增,則
上單調遞增,則![]() ,等價于
,等價于![]() ,即
,即![]() ,再分離參數得
,再分離參數得![]() ,由不等式恒成立問題,從而可得解.
,由不等式恒成立問題,從而可得解.
試題解析:(Ⅰ)∵函數![]() 的定義域為R,且
的定義域為R,且![]() 是奇函數,∴
是奇函數,∴![]() ,解得
,解得![]()
此時![]() ,滿足
,滿足![]() ,即
,即![]() 是奇函數.
是奇函數.
∴![]() . …… 4分
. …… 4分
(Ⅱ) 任取![]() ,且
,且![]() ,則
,則![]() ,
,![]() ,
,
于是![]()
即![]() ,故函數
,故函數![]() 在
在![]() 上是增函數. …… 8分
上是增函數. …… 8分
(Ⅲ)由![]() 及
及![]() 是奇函數,知
是奇函數,知![]()
又由![]() 在
在![]() 上是增函數,得
上是增函數,得![]() ,即
,即![]() 對任意的
對任意的![]() 恒成立
恒成立
∵當![]() 時,
時,![]() 取最小值
取最小值![]() ,∴
,∴![]() …… 12分
…… 12分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】下面是一個2×2列聯表,則表中a、b的值分別為 ( )
y1 | y2 | 合計 | |
x1 | a | 21 | 73 |
x2 | 2 | 25 | 27 |
合計 | b | 46 | 100 |
A. 94、96 B. 52、50
C. 52、54 D. 54、52
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,G為ABC的重心,延長線段AG交BC于F,B1F交BC1于E.
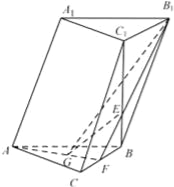
(1)求證:GE∥平面AA1B1B;
(2)平面AFB1分此棱柱為兩部分,求這兩部分體積的比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知方程![]() .
.
(1)若此方程表示圓,求![]() 的取值范圍;
的取值范圍;
(2)若(1)中的圓與直線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() ;
;
(3)在(2)的條件下,求以![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將正整數排成下表:
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
……………
則在表中數字2017出現在( )
A. 第44行第80列 B. 第45行第80列 C. 第44行第81列 D. 第45行第81列
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com