
已知橢圓C的方程為![]() ,雙曲線
,雙曲線![]() 的兩條漸近線為l1,l2,過橢圓C的右焦點F作直線l,使l⊥l1,又l與l2交于P,設(shè)l與橢圓C的兩個交點由上至下依次為A、B(如圖).
的兩條漸近線為l1,l2,過橢圓C的右焦點F作直線l,使l⊥l1,又l與l2交于P,設(shè)l與橢圓C的兩個交點由上至下依次為A、B(如圖).
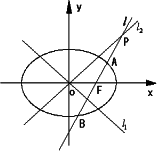
(1)當(dāng)l1與l2的夾角為60°,且△POF的面積為![]() 時,求橢圓C的方程;
時,求橢圓C的方程;
(2)當(dāng)![]() 時,求
時,求![]() 的最大值.
的最大值.
解:(1)l1的斜率為![]() ,l2的斜率為
,l2的斜率為![]() ,由l1與l2的夾角為60°,得
,由l1與l2的夾角為60°,得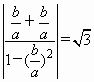 .
.
整理,得![]() .①
.①
由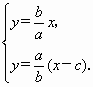 得
得![]() .由
.由![]() ,得
,得![]() .
.
∴![]() .②
.②
由①②,解得![]() ,b=1.∴橢圓C方程為:
,b=1.∴橢圓C方程為:![]() .
.
(2)由![]() ,F(xiàn)(c,0)及
,F(xiàn)(c,0)及![]() ,得
,得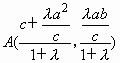 .
.
將A點坐標(biāo)代入橢圓方程,得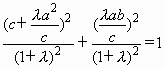 .
.
整理,得![]() ,
,
∴![]() 的最大值為
的最大值為![]() ,此時
,此時![]() .
.
分析:(1)求橢圓方程即求a、b.根據(jù)題中的兩個數(shù)量關(guān)系:l1與l2的夾角為60°,△POF的面積為![]() ,列出關(guān)于a、b的兩個方程即可.
,列出關(guān)于a、b的兩個方程即可.
(2)由P、F的坐標(biāo)求出A點的坐標(biāo),代入橢圓方程可得![]() 與a、b、c的關(guān)系,進而得出
與a、b、c的關(guān)系,進而得出![]() 與離心率e的關(guān)系.
與離心率e的關(guān)系.
說明:本題考查綜合運用解析幾何知識解決問題的能力,重點考查在圓錐曲線中解決問題的基本方法,轉(zhuǎn)化能力,以及字母運算的能力.


 小學(xué)奪冠AB卷系列答案
小學(xué)奪冠AB卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| ||
| 3 |
| 13 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| a2 |
| y2 |
| 2 |
| ||
| 2 |
| OP |
| OM |
| ON |
| 1 |
| 2 |
| y | 2 0 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
| a2 |
| c |
| ||
| 2 |
| AP |
| PB |
| OA |
| OB |
| OP |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x 2 |
| 4 |
| y2 |
| 3 |
| m |
| OA |
| OB |
| m |
| OF |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com