
(本題14分)口袋內有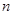 (
(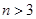 )個大小相同的球,其中有3個紅球和
)個大小相同的球,其中有3個紅球和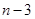 個白球.已知從
個白球.已知從
口袋中隨機取出一個球是紅球的概率是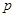 ,且
,且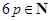 。若有放回地從口袋中連續地取四次球(每次只取一個球),在四次取球中恰好取到兩次紅球的概率大于
。若有放回地從口袋中連續地取四次球(每次只取一個球),在四次取球中恰好取到兩次紅球的概率大于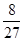 。
。
(Ⅰ)求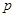 和
和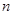 ;
;
(Ⅱ)不放回地從口袋中取球(每次只取一個球),取到白球時即停止取球,記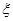 為第一次取到白球時的取球次數,求
為第一次取到白球時的取球次數,求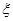 的分布列和期望
的分布列和期望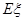 。
。
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013屆浙江桐鄉高級中學高二第二學期期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分14分)
一個口袋內有4個不同的紅球,6個不同的白球.
(1)從中任取4個球,紅球的個數不比白球少的取法有多少種?
(2)若取一個紅球記2分,取一個白球記1分,從中任取4個球,使總分不少于7分的取法有多少種?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com