【題目】已知函數
.
（1）若曲線
在
處切線的斜率為
，求此切線方程；
（2）若
有兩個極值點
，求
的取值范圍，并證明：
.
【答案】(1) 
.
(2)見解析.
【解析】分析：第一問首先利用導數的幾何意義以及切點既在切線上，又在函數圖像上，從而利用相應的公式求得切線方程；第二問從函數有兩個極值點，對應的是其導數等于零有兩個不相等的正根，構造新函數，利用導數研究其走向，分類討論證得結果.
詳解：（1）∵
，∴
，解得
，
∴
，故切點為
，
所以曲線
在
處的切線方程為．
（2），令
，得
．
令
，則
，
且當
時，
；當
時，
；
時，
．
令
，得，
且當
時，
；當
時，
．
故
在
遞增，在
遞減，所以
．
所以當
時，
有一個極值點；
時，有兩個極值點；
當
時，沒有極值點．
綜上，
的取值范圍是
．
因為
是的兩個極值點，所以
即
…①
不妨設
，則
，
，
因為在
遞減，且
，所以
，即
…②．
由①可得
，即
，
由①，②得
，所以
．
科目：高中數學 來源： 題型：
【題目】在全國第五個“扶貧日”到來之前,某省開展“精準扶貧,攜手同行”的主題活動,某貧困縣調查基層干部走訪貧困戶數量．
鎮有基層干部60人,
鎮有基層干部60人,
鎮有基層干部80人,每人都走訪了若干貧困戶,按照分層抽樣,從
三鎮共選40名基層干部,統計他們走訪貧困戶的數量,并將走訪數量分成5組,
,繪制成如圖所示的頻率分布直方圖．
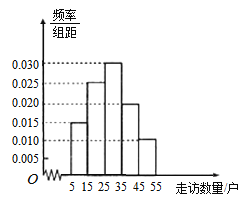
(1)求這40人中有多少人來自鎮,并估計三鎮的基層干部平均每人走訪多少貧困戶；(同一組中的數據用該組區間的中點值作代表)
(2)如果把走訪貧困戶達到或超過25戶視為工作出色,以頻率估計概率,從三鎮的所有基層干部中隨機選取3人,記這3人中工作出色的人數為
,求的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率是
，過點
作斜率為
的直線
交橢圓
于
兩點，當直線垂直于
軸時，
．
（1）求橢圓的方程
（2）當變化時，在
軸上是否存在點
，使得
是以
為底的等腰三角形？若存在，求出
的取值范圍；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲，乙二人進行乒乓球比賽，已知每一局比賽甲勝乙的概率是
，假設每局比賽結果相互獨立.
(Ⅰ)比賽采用三局兩勝制，即先獲得兩局勝利的一方為獲勝方，這時比賽結束．求在一場比賽中甲獲得比賽勝利的概率；
(Ⅱ)比賽采用三局兩勝制，設隨機變量
為甲在一場比賽中獲勝的局數，求的分布列和均值；
(Ⅲ)有以下兩種比賽方案：方案一，比賽采用五局三勝制；方案二，比賽采用七局四勝制.問哪個方案對甲更有利.（只要求直接寫出結果）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】長沙某公司生產一種高科技晶片100片，生產過程中由于受到一些不可抗因素的影響，晶片會受到一定程度的磨損，因此在生產結束之后需要由測試人員進行相應的指標測試.指標測試情況統計如表所示：
若
，則稱該晶片為合格品，否則該晶片為劣質品.
（1）試求本次生產過程中該公司生產出合格品的頻率以及數量；
（2）求這批晶片測試指標的平均值；
（3）現按照分層抽樣的方法在測試指標在
與
之間的晶片中抽取6個晶片，再從這6個晶片中任取2個晶片進入深入分析，求恰有1個晶片的測試指標在之間的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某單位甲、乙、丙三個部門的員工人數分別為24，16，16.現采用分層抽樣的方法從中抽取7人，進行睡眠時間的調查.
（1）應從甲、乙、丙三個部門的員工中分別抽取多少人？
（2）若抽出的7人中有4人睡眠不足，3人睡眠充足，現從這7人中隨機抽取3人做進一步的身體檢查.用X表示抽取的3人中睡眠不足的員工人數，求隨機變量X的分布列與數學期望；
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設全集U=R，集合A={x|1≤x＜4}，B={x|2a≤x＜3-a}．
（1）若a=-2，求B∩A，B∩(UA)；（2）若A∪B=A，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
