
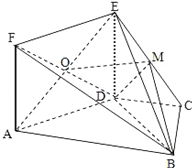
【題目】如圖,邊長為![]() 的正方形
的正方形![]() 與梯形
與梯形![]() 所在的平面互相垂直,其中
所在的平面互相垂直,其中![]() ,
, ![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(Ⅰ)推導(dǎo)出OM∥AC,由此根據(jù)線面平行的判定定理能證明OM||平面ABCD.(Ⅱ)推導(dǎo)出BD⊥DA,因為平面ADEF⊥平面ABCD,從而可得BD⊥平面ADEF,由此得到∠BFD的余弦值即為所求.
試題解析:
證明:(Ⅰ)∵O,M分別為EA,EC的中點(diǎn), ∴OM∥AC.
∵OM![]() 平面ABCD,AC
平面ABCD,AC![]() 平面ABCD….∴OM∥平面ABCD
平面ABCD….∴OM∥平面ABCD
解:(Ⅱ) ∵DC=BC=1,∠BCD=90°,
∴![]() ∵
∵![]() . ∴BD⊥DA.
. ∴BD⊥DA.
∵平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,BD平面ABCD,
∴BD⊥平面ADEF
∴∠BFD的余弦值即為所求.
在![]() ,
,
∴![]() ….
….
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() .
.
⑴ 若直線![]() 與曲線
與曲線![]() 恒相切于同一定點(diǎn),求
恒相切于同一定點(diǎn),求![]() 的方程;
的方程;
⑵ 若![]() ,求證:當(dāng)
,求證:當(dāng)![]() 時,
時, ![]() 恒成立;
恒成立;
⑶ 若當(dāng)![]() 時,
時, ![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下表提供了某廠節(jié)能降耗技術(shù)改造后生產(chǎn)甲產(chǎn)品過程中記錄的產(chǎn)量x(噸)與相應(yīng)的生產(chǎn)能耗y(噸標(biāo)準(zhǔn)煤)的幾組對照數(shù)據(jù).
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)請畫出上表數(shù)據(jù)的散點(diǎn)圖;
(2)請根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出y關(guān)于x的線性回歸方程![]() ;
;
(3)已知該廠技改前100噸甲產(chǎn)品的生產(chǎn)能耗為90噸標(biāo)準(zhǔn)煤.試根據(jù)(2)求出的線性回歸方程,預(yù)測生產(chǎn)100噸甲產(chǎn)品的生產(chǎn)能耗比技改前降低多少噸標(biāo)準(zhǔn)煤.
(參考數(shù)值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求曲線在
,求曲線在![]() 點(diǎn)處的切線方程;
點(diǎn)處的切線方程;
(2)若曲線![]() 與直線
與直線![]() 只有一個交點(diǎn),求實(shí)數(shù)
只有一個交點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,則(ⅰ)
,則(ⅰ)![]() ____________.
____________.
(ⅱ)給出下列三個命題:①函數(shù)![]() 是偶函數(shù);②存在
是偶函數(shù);②存在![]() ,使得以點(diǎn)
,使得以點(diǎn)![]() 為頂點(diǎn)的三角形是等腰三角形;③存在
為頂點(diǎn)的三角形是等腰三角形;③存在![]() ,使得以點(diǎn)
,使得以點(diǎn)![]() 為頂點(diǎn)的四邊形為菱形.
為頂點(diǎn)的四邊形為菱形.
其中,所有真命題的序號是____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() R
R![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的最小值;
的最小值;
(2)若對任意![]() ,恒有
,恒有![]() 成立,求實(shí)數(shù)
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在R的函數(shù)![]() 是偶函數(shù),且滿足
是偶函數(shù),且滿足![]() 上的解析式為
上的解析式為![]() ,過點(diǎn)
,過點(diǎn)![]() 作斜率為k的直線l,若直線l與函數(shù)
作斜率為k的直線l,若直線l與函數(shù)![]() 的圖象至少有4個公共點(diǎn),則實(shí)數(shù)k的取值范圍是
的圖象至少有4個公共點(diǎn),則實(shí)數(shù)k的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校高一年級開設(shè)![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五門選修課,每位同學(xué)須彼此獨(dú)立地選三課程,其中甲同學(xué)必選
五門選修課,每位同學(xué)須彼此獨(dú)立地選三課程,其中甲同學(xué)必選![]() 課程,不選
課程,不選![]() 課程,另從其余課程中隨機(jī)任選兩門課程.乙、丙兩名同學(xué)從五門課程中隨機(jī)任選三門課程.
課程,另從其余課程中隨機(jī)任選兩門課程.乙、丙兩名同學(xué)從五門課程中隨機(jī)任選三門課程.
(Ⅰ)求甲同學(xué)選中![]() 課程且乙同學(xué)未選中
課程且乙同學(xué)未選中![]() 課程的概率.
課程的概率.
(Ⅱ)用![]() 表示甲、乙、丙選中
表示甲、乙、丙選中![]() 課程的人數(shù)之和,求
課程的人數(shù)之和,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com