
如圖,在四面體ABCD中,P、Q分別為棱BC與CD上的點,且BP=2PC,CQ=2QD.R為棱AD的中點,則點A、B到平面PQR的距離的比值為 .
.
:A、B到平面PQR的距離分別為三棱錐APQR與BPQR的以三角形PQR為底的高.故其比值等于這兩個三棱錐的體積比.
VAPQR=VAPQD=×VAPCD=××VABCD=VABCD;
又,SBPQ=SBCD-SBDQ-SCPQ=(1--×)SBCD=SBCD,
VRBPQ=VRBCD=×VABCD=VABCD.∴ A、B到平面PQR的距離的比=1∶4.
又,可以求出平面PQR與AB的交點來求此比值:
在面BCD內,延長PQ、BD交于點M,則M為面PQR與棱BD的交點.
 由Menelaus定理知,··=1,而=,=,故=4.
由Menelaus定理知,··=1,而=,=,故=4.
在面ABD內,作射線MR交AB于點N,則N為面PQR與AB的交點.
由Menelaus定理知,··=1,而=4,=1,故=.
∴ A、B到平面PQR的距離的比=1∶4.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
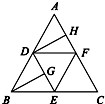 如圖,在正三角形ABC中,D,E,F分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為
如圖,在正三角形ABC中,D,E,F分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為查看答案和解析>>
科目:高中數學 來源: 題型:
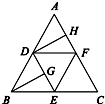 如圖,在正三角形ABC中,D,E,F分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為( )
如圖,在正三角形ABC中,D,E,F分別為各邊的中點,G,H分別為DE,AF的中點,將△ABC沿DE,EF,DF折成正四面體P-DEF,則四面體中異面直線PG與DH所成的角的余弦值為( )查看答案和解析>>
科目:高中數學 來源: 題型:
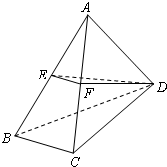 如圖,在四面體ABCD中,BC⊥面ACD,DA=DC,E、F分別為AB、AC的中點.
如圖,在四面體ABCD中,BC⊥面ACD,DA=DC,E、F分別為AB、AC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
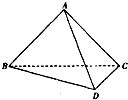 (2009•武漢模擬)如圖,在四面體A-BCD中,AB=AD=
(2009•武漢模擬)如圖,在四面體A-BCD中,AB=AD=| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
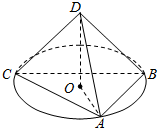 如圖,在四面體ABCD中,DA=DB=DC=1,且DA,DB,DC兩兩互相垂直,點O是△ABC的中心,將△DAO繞直線DO旋轉一周,則在旋轉過程中,直線DA與BC所成角的余弦值的取值范圍是( )
如圖,在四面體ABCD中,DA=DB=DC=1,且DA,DB,DC兩兩互相垂直,點O是△ABC的中心,將△DAO繞直線DO旋轉一周,則在旋轉過程中,直線DA與BC所成角的余弦值的取值范圍是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com