
【題目】已知函數f(x)=|3x﹣1|﹣2|x|+2.
(1)解不等式:f(x)<10;
(2)若對任意的實數x,f(x)﹣|x|≤a恒成立,求實數a的取值范圍.
【答案】
(1)解:x<0時,不等式化為﹣3x+1+2x+2<10,解得x>﹣7,∴﹣7<x<0;
0 ![]() 時,不等式化為﹣3x+1﹣2x+2<10,解得x>﹣
時,不等式化為﹣3x+1﹣2x+2<10,解得x>﹣ ![]() ,∴0
,∴0 ![]() ;
;
x> ![]() 時,不等式化為3x﹣1﹣2x+2<10,解得x<9,∴
時,不等式化為3x﹣1﹣2x+2<10,解得x<9,∴ ![]() ;
;
綜上所述,不等式的解集為(﹣7,9);
(2)解:對任意的實數x,f(x)﹣|x|≤a恒成立,即|3x﹣1|﹣|3x|≤a﹣2,
∵|3x﹣1|﹣|3x|≤|3x﹣1﹣3x|=1,
∴a﹣2≥1,∴a≥3.
【解析】(1)分類討論,解不等式:f(x)<10;(2)對任意的實數x,f(x)﹣|x|≤a恒成立,即|3x﹣1|﹣|3x|≤a﹣2,利用|3x﹣1|﹣|3x|≤|3x﹣1﹣3x|=1,即可求實數a的取值范圍.
【考點精析】解答此題的關鍵在于理解絕對值不等式的解法的相關知識,掌握含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求月平均用電量的平均數、眾數和中位數;
(3)在月平均用電量為,![]() ,
,![]() ,
,![]() ,
,![]() 的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在
的四組用戶中,用分層抽樣的方法抽取11戶居民,則月平均用電量在![]() 的用戶中應抽取多少戶?
的用戶中應抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ACDE所在的平面與平面ABC垂直,M是CE和AD的交點,AC![]() BC,且AC=BC.
BC,且AC=BC.
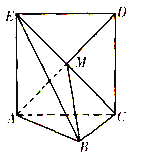
(1)求證:AM![]() 平面EBC;
平面EBC;
(2)求直線AB與平面EBC所成角的大小,
(3)求二面角A-BE-C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了政府對過熱的房地產市場進行調控決策,統計部門對城市人和農村人進行了買房心理預測調研,用簡單隨機抽樣的方法抽取了110人進行統計,得到如下列聯表:
買房 | 不買房 | 糾結 | |
城市人 | 5 | 15 | |
農村人 | 20 | 10 |
已知樣本中城市人數與農村人數之比是3:8.
(Ⅰ)分別求樣本中城市人中的不買房人數和農村人中的糾結人數;
(Ⅱ)從參與調研的城市人中用分層抽樣方法抽取6人,進一步統計城市人的某項收入指標,假設一個買房人的指標算作3,一個糾結人的指標算作2,一個不買房人的指標算作1,現在從這6人中再隨機選取3人,令X=再抽取3人指標之和,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校從高一年級學生中隨機抽取40名學生,將他們的期中考試數學成績(滿分100分,成績均為不低于40分的整數)分成六段:[40,50),[50,60),…,[90,100]后得到如圖所示的頻率分布直方圖,其中前三段的頻率成等比數列. 
(1)求圖中實數a的值;
(2)若該校高一年級共有學生640人,試估計該校高一年級期中考試數學成績不低于80分的人數;
(3)若從樣本中數學成績在[40,50)與[90,100]兩個分數段內的學生中隨機選取兩名學生,記這兩名學生成績在[90,100]內的人數為X,求隨機變量X的分布列和期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若曲線f(x)= ![]() (e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分別存在點A、B,使得△OAB是以原點O為直角頂點的直角三角形,且斜邊AB的中點在y軸上,則實數a的取值范圍是( )
(e﹣1<x<e2﹣1)和g(x)=﹣x3+x2(x<0)上分別存在點A、B,使得△OAB是以原點O為直角頂點的直角三角形,且斜邊AB的中點在y軸上,則實數a的取值范圍是( )
A.(e,e2)
B.(e, ![]() )
)
C.(1,e2)
D.[1,e)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=e2x , g(x)=kx+1(k∈R). (Ⅰ)若直線y=g(x)和函數y=f(x)的圖象相切,求k的值;
(Ⅱ)當k>0時,若存在正實數m,使對任意x∈(0,m),都有|f(x)﹣g(x)|>2x恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐A﹣BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE. 
(1)若F是AD的中點,求證:EF∥平面ABC;
(2)若AD=DE,求BE與平面ACE所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com