
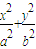 =1(a>b>0)的離心率為e=
=1(a>b>0)的離心率為e=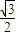 ,直線l被圓O截得的弦長與橢圓的長軸長相等.
,直線l被圓O截得的弦長與橢圓的長軸長相等.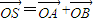 (O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.
(O是坐標原點),是否存在這樣的直線l,使四邊形為ASB的對角線長相等?若存在,求出直線l的方程,若不存在,說明理由.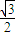 ,即可求得橢圓C的方程;
,即可求得橢圓C的方程;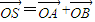 ,可得四邊形OASB是平行四邊形.假設存在這樣的直線l,使四邊形OASB的對角線長相等,則四邊形OASB為矩形,因此有
,可得四邊形OASB是平行四邊形.假設存在這樣的直線l,使四邊形OASB的對角線長相等,則四邊形OASB為矩形,因此有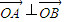 ,設直線方程代入橢圓方程,利用向量的數量積公式,即可求得結論.
,設直線方程代入橢圓方程,利用向量的數量積公式,即可求得結論.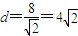 ,
,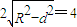 ,
,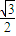 ,
,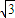
 ; …(4分)
; …(4分)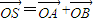 ,∴四邊形OASB是平行四邊形.
,∴四邊形OASB是平行四邊形.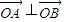 ,
,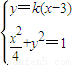 ,得(1+4k2)x2-24k2x+36k2-4=0,
,得(1+4k2)x2-24k2x+36k2-4=0,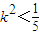 .…(9分)
.…(9分)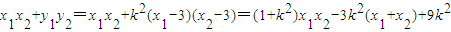 =
=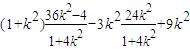 ,
,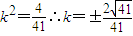 ,滿足△>0.…(12分)
,滿足△>0.…(12分) .…(13分)
.…(13分)

科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OQ |
| a |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com