【題目】在如圖所示的三棱錐
中，
底面
分別是
的中點．
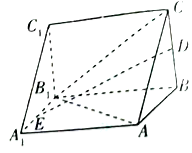
（1）求證：
平面
；
（2）若
，求直線
與平面
所成角的正切值．
【答案】（1）證明見解析；（2）
.
【解析】
試題分析：（1）借助題設條件運用線面平行的判定定理求解；（2）借助題設運用直線與平面所成角的定義找出其角,再運用解三角形的方法求解.
試題解析：（1）取
的中點
，連接
在
中，因為
分別為
的中點，
所以
平面
平面
，
所以
平面
在矩形
中，因為
分別為
的中點，
所以
平面 
平面，所以
平面
因為
，所以平面
平面
因為
平面
，所以
平面
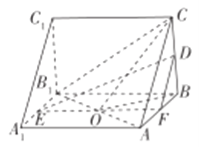
（2）因為三棱柱
為直三棱柱，所以
，
又
，所以
平面
，
因為
，所以
，
又
，所以
為正三角形，
所以
，所以
取
的中點
，連接
，所以
，所以
平面
，
所以平面
平面
，點
在平面
上的射影在
上，
所以
即為直線
與平面
所成角
在
中，
，所以
．．．．．．．．．12分
（若用空間向量處理，請相應給分）
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某校對高一年級學生寒假參加社區服務的次數進行了統計，隨機抽取了
名學生作為樣本，得到這
名學生參加社區服務的次數，根據此數據作出了頻率分布統計表和頻率分布直方圖如下：
（1）求表中
的值和頻率分布直方圖中
的值，并根據頻率分布直方圖估計該校高一學生寒假參加社區服務次數的中位數；
（2）如果用分層抽樣的方法從樣本服務次數在
和
的人中共抽取6人，再從這6人中選2人，求2人服務次數都在的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等邊三角形，已知AD=4， 
，AB=2CD=8．
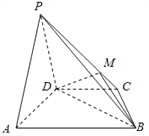
（1）設M是PC上的一點，證明：平面MBD⊥平面PAD；
（2）當M點位于線段PC什么位置時，PA∥平面MBD？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在以
為頂點的五面體中，O為AB的中點，
平面
， 
∥
， 
， 
， 
．
（1）在圖中過點O作平面
，使得
∥平面
，并說明理由；
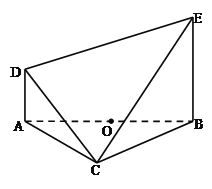
（2）求直線DE與平面CBE所成角的正切值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有兩個不透明的箱子，每個箱子都裝有4個完全相同的小球，球上分別標有數字1,2,3,4.
(1)甲從其中一個箱子中摸出一個球，乙從另一個箱子摸出一個球，誰摸出的球上標的數字大誰就獲勝（若數字相同則為平局），求甲獲勝的概率；
(2)摸球方法與（1）同，若規定：兩人摸到的球上所標數字相同甲獲勝，所標數字不相同則乙獲勝，這樣規定公平嗎？請說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
（1）求函數
的單調遞減區間；
（2）若關于
的方程
在區間
上有兩個不等的根，求實數
的取值范圍；
（3）若存在
，當
時，恒有
，求實數
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
