在△ABC中,內角A、B、C的對邊長分別為a、b、c,已知a2-c2=2b,且sinAcosC=3cosAsinC,求b
【答案】
分析:根據正弦定理和余弦定理將sinAcosC=3cosAsinC化成邊的關系,再根據a
2-c
2=2b即可得到答案.
解答:解:法一:在△ABC中∵sinAcosC=3cosAsinC,
則由正弦定理及余弦定理有:
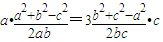
,
化簡并整理得:2(a
2-c
2)=b
2.
又由已知a
2-c
2=2b∴4b=b
2.
解得b=4或b=0(舍);
法二:由余弦定理得:a
2-c
2=b
2-2bccosA.
又a
2-c
2=2b,b≠0.
所以b=2ccosA+2①又sinAcosC=3cosAsinC,
∴sinAcosC+cosAsinC=4cosAsinCsin(A+C)=4cosAsinC,
即sinB=4cosAsinC由正弦定理得
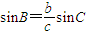
,
故b=4ccosA②由①,②解得b=4.
點評:本題主要考查正弦定理和余弦定理的應用.屬基礎題.

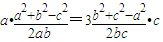 ,
,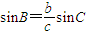 ,
,

 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案