【題目】為了迎接第二屆國際互聯網大會，組委會對報名參加服務的
名志愿者進行互聯網知識測試，從這
名志愿者中采用隨機抽樣的方法抽取
人，所得成績如下： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
.
（1）作出抽取的
人的測試成績的莖葉圖，以頻率為概率，估計這
志愿者中成績不低于
分的人數；
（2）從抽取的成績不低于
分的志愿者中，隨機選
名參加某項活動，求選取的
人恰有一人成績不低于
分的概率.
【答案】(1) 
；(2) 
.
【解析】試題分析：（Ⅰ）根據成績，莖為十位數字5,6,7,8,9，個數數字為葉，得莖葉圖，由樣本得成績在90以上頻率為
，由此可估計出成績不低于90分的人數；（Ⅱ）抽取的成績不低于80分的志愿者有6人，從中選3人可有20種選法（可用列舉法列出各種可能），然后再數出恰有一人成績不低于90分的有12種，由概率公式可得概率．
試題解析：（Ⅰ）抽取的15人的成績莖葉圖如圖所示，
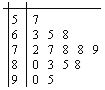
由樣本得成績在90以上頻率為
，故志愿者測試成績在90分以上（包含90分）的人數約為
=200人.
（Ⅱ）設抽取的15人中，成績在80分以上（包含80分）志愿者為
, 
, 
, 
, 
, 
,其中
， 
的成績在90分以上（含90分），
成績在80分以上（包含80分）志愿者中隨機選3名志愿者的不同選法有：{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
, 
, 
},{ 
, 
, 
},{ 
, 
, 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
},{ 
， 
， 
}共20種，
其中選取的3人中恰有一人成績在90分以上的不同取法有：{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
, 
, 
},{ 
, 
, 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}，{ 
， 
， 
}共12種，
∴選取的3人中恰有一人成績在90分以上的概率為
=
.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】下列事件是隨機事件的是（ ）
①當x>10時，
； ②當x∈R，x2+x＝0有解
③當a∈R關于x的方程x2+a＝0在實數集內有解； ④當sinα>sinβ時，α>β（ ）
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在對人們的休閑方式的一次調查中，用簡單隨機抽樣方法調查了125人，其中女性70人，男性55人.女性中有40人主要的休閑方式是看電視，另外30人主要的休閑方式是運動；男性中有20人主要的休閑方式是看電視，另外35人主要的休閑方式是運動.
（1）根據以上數據建立一個
列聯表；
（2）能否在犯錯誤的概率不超過0.025的前提下，認為性別與休閑方式有關系?
（3）在休閑方式為看電視的人中按分層抽樣方法抽取6人參加某機構組織的健康講座，講座結束后再從這6人中抽取2人作反饋交流，求參加交流的恰好為2位女性的概率.
附：
P（ | 0.05 | 0.025 | 0.010 |
k | 3.841 | 5.024 | 6.635 |
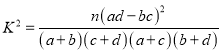
休閑方式 性別 | 看電視 | 運動 | 合計 |
女 | |||
男 | |||
合計 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某區“創文明城區”（簡稱“創城”）活動中，教委對本區
四所高中學校按各校人數分層抽樣，隨機抽查了100人，將調查情況進行整理后制成下表：
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
（注：參與率是指：一所學校“創城”活動中參與的人數與被抽查人數的比值）假設每名高中學生是否參與”創城”活動是相互獨立的.
（1）若該區共2000名高中學生，估計
學校參與“創城”活動的人數；
（2）在隨機抽查的100名高中學生中，隨機抽取1名學生，求恰好該生沒有參與“創城”活動的概率；
（3）在上表中從
兩校沒有參與“創城”活動的同學中隨機抽取2人，求恰好兩校各有1人沒有參與“創城”活動的概率是多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
