
【題目】已知數列{an}滿足Sn+an=2n+1.
(1)寫出a1 , a2 , a3 , 并推測an的表達式;
(2)用數學歸納法證明所得的結論.
【答案】
(1)解:當n=1,時S1+a1=2a1=3
∴a1= ![]()
當n=2時,S2+a2=a1+a2+a2=5
∴a2= ![]() ,
,
同樣令n=3,則可求出a3= ![]()
∴a1= ![]() ,a2=
,a2= ![]() ,a3=
,a3= ![]()
猜測an=2﹣ ![]()
(2)解:①由(1)已得當n=1時,命題成立;
②假設n=k時,命題成立,即ak=2﹣ ![]() ,
,
當n=k+1時,a1+a2+…+ak+2ak+1=2(k+1)+1,
且a1+a2+…+ak=2k+1﹣ak
∴2k+1﹣ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2﹣ ![]() ,即ak+1=2﹣
,即ak+1=2﹣ ![]() ,
,
即當n=k+1時,命題成立.
根據①②得n∈N+,an=2﹣ ![]() 都成立.
都成立.
【解析】(1)取n=1,2,3,分別求出a1 , a2 , a3 , 然后仔細觀察,總結規律,猜測an的值.(2)用數學歸納法進行證明,①當n=1時,命題成立;②假設n=k時,命題成立,即ak=2﹣ ![]() ,當n=k+1時,a1+a2+…+ak+ak+1+ak+1=2(k+1)+1,ak+1=2﹣
,當n=k+1時,a1+a2+…+ak+ak+1+ak+1=2(k+1)+1,ak+1=2﹣ ![]() ,當n=k+1時,命題成立.故an=2﹣
,當n=k+1時,命題成立.故an=2﹣ ![]() 都成立.
都成立.
【考點精析】本題主要考查了數列的通項公式和數學歸納法的定義的相關知識點,需要掌握如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式;數學歸納法是證明關于正整數n的命題的一種方法才能正確解答此題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】現有![]() (n≥2,n∈N*)個給定的不同的數隨機排成一個下圖所示的三角形數陣:
(n≥2,n∈N*)個給定的不同的數隨機排成一個下圖所示的三角形數陣:

設Mk是第k行中的最大數,其中1≤k≤n,k∈N*.記M1<M2<…<Mn的概率為pn.
(1)求p2的值;
(2)證明:pn>![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點E. 
(1)若D為AC的中點,證明:DE是⊙O的切線;
(2)若OA= ![]() CE,求∠ACB的大小.
CE,求∠ACB的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于R上的可導函數f(x),若a>b>1且有(x﹣1)f′(x)≥0,則必有( )
A.f(a)+f(b)<2f(1)
B.f(a)+f(b)≤2f(1)
C.f(a)+f(b)≥2f(1)
D.f(a)+f(b)>2f(1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個小組各10名學生的英語口語測試成績的莖葉圖如圖所示,現從這20名學生中隨機抽取一人,將“抽出的學生為甲小組學生”記為事件A;“抽出的學生英語口語測試成績不低于85分”記為事件B.則P(A|B)=( )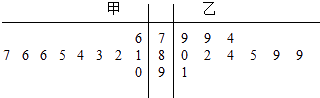
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:設![]() 為
為![]() 上的可導函數,若
上的可導函數,若![]() 為增函數,則稱
為增函數,則稱![]() 為
為![]() 上的凸函數.
上的凸函數.
(1)判斷函數![]() 與
與![]() 是否為凸函數;
是否為凸函數;
(2)設![]() 為
為![]() 上的凸函數,求證:若
上的凸函數,求證:若![]() ,
, ![]() ,則
,則![]() 恒有
恒有![]() 成立;
成立;
(3)設![]() ,
, ![]() ,
, ![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin( ![]() ﹣φ)(0<φ<
﹣φ)(0<φ< ![]() )的圖象經過點(0,﹣1).
)的圖象經過點(0,﹣1).
(1)求函數f(x)的對稱軸方程及相鄰兩條對稱軸間的距離d;
(2)設α、β∈[0, ![]() ],f(3α+
],f(3α+ ![]() )=
)= ![]() ,f(3β+2π)=
,f(3β+2π)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com