
【題目】已知全集U={x|x2﹣3x+2≥0},A={x||x﹣2|>1},B= ![]()
求:
(1)A∩B;
(2)A∩UB;
(3)U(A∪B).
【答案】
(1)解:由U=x|x2﹣3x+2≥0
化簡得:U={x|x≤1或x≥2}
由A=x||x﹣2|>1
化簡得:A={x|x<1或x>3}
由B= ![]()
化簡得:B={x|x<1或x>2}
A∩B={x|x<1或x>3}
(2)解:CUB={1,2}
A∩CUB=
(3)解:A∪B={x|x<1或x>2}
CU(A∪B)={1,2}
【解析】根據 ![]() ,分別進行化簡,然后①直接求A∩B,②先求CUB再求A∩CUB,③先求A∪B,再求CU(A∪B.
,分別進行化簡,然后①直接求A∩B,②先求CUB再求A∩CUB,③先求A∪B,再求CU(A∪B.
【考點精析】掌握集合的并集運算和集合的交集運算是解答本題的根本,需要知道并集的性質:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,則A
=A,A∪B=B∪A;(2)若A∪B=B,則A![]() B,反之也成立;交集的性質:(1)A∩B
B,反之也成立;交集的性質:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,則A
,A∩B=B∩A;(2)若A∩B=A,則A![]() B,反之也成立.
B,反之也成立.


科目:高中數學 來源: 題型:
【題目】如圖,一條河的兩岸平行,河的寬度d=600m,一艘客船從碼頭A出發勻速駛往河對岸的碼頭B.已知|AB|=1km,水流速度為2km/h, 若客船行駛完航程所用最短時間為6分鐘,則客船在靜水中的速度大小為( )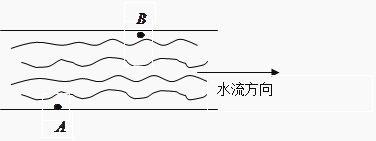
A.8km/h
B.![]() km/h
km/h
C.![]() km/h
km/h
D.10km/h
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
已知直線l的參數方程為 (t為參數),曲線C的參數方程為
(t為參數),曲線C的參數方程為 (θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點P的極坐標為
(θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,點P的極坐標為![]() 。
。
(Ⅰ)求直線l以及曲線C的極坐標方程;
(Ⅱ)設直線l與曲線C交于A,B兩點,求△PAB的面積。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點A(0,1),B(0,﹣1),C(1,0),動點P滿足: ![]() ,
,
(1)求動點P的軌跡方程,并說明方程表示的曲線類型;
(2)當k=2,求![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個結論,其中正確的個數為( ). ①已 ![]() ,則
,則 ![]()
②過原點作曲線 ![]() 的切線,則切線方程為
的切線,則切線方程為 ![]() (其中e為自然對數的底數);
(其中e為自然對數的底數);
③已知隨機變 ![]()
![]() ,則
,則 ![]()
④已知n為正偶數,用數學歸納法證明等式 ![]() 時,若假設
時,若假設 ![]() 時,命題為真,則還需利用歸納假設再證明
時,命題為真,則還需利用歸納假設再證明 ![]() 時等式成立,即可證明等式對一切正偶數n都成立.
時等式成立,即可證明等式對一切正偶數n都成立.
⑤在回歸分析中,常用 ![]() 來刻畫回歸效果,在線性回歸模型中,
來刻畫回歸效果,在線性回歸模型中, ![]() 表示解釋變量對于預報變量變化的貢獻率
表示解釋變量對于預報變量變化的貢獻率 ![]() 越接近1,表示回歸的效果越好.
越接近1,表示回歸的效果越好.
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com