
【題目】已知函數![]() .
.
(1)若![]() ,解不等式
,解不等式![]() ;
;
(2)若存在實數![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)由絕對值定義將不等式化為三個不等式組,分別求解集,最后求并集(2)先化簡不等式為|3x﹣a|﹣|3x+6|≥1﹣a,再根據絕對值三角不等式得|3x﹣a|﹣|3x+6|最大值為|a+6|,最后解不等式得實數![]() 的取值范圍
的取值范圍
試題解析:解:(1)a=2時:f(x)=|3x﹣2|﹣|x+2|≤3,
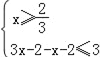 或
或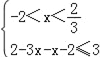 或
或![]() ,
,
解得:﹣![]() ≤x≤
≤x≤![]() ;
;
(2)不等式f(x)≥1﹣a+2|2+x|成立,
即|3x﹣a|﹣|3x+6|≥1﹣a,
由絕對值不等式的性質可得||3x﹣a|﹣|3x+6||≤|(3x﹣a)﹣(3x+6)|=|a+6|,
即有f(x)的最大值為|a+6|,
∴![]() 或
或![]() ,
,
解得:a≥﹣![]() .
.


科目:高中數學 來源: 題型:
【題目】某電動小汽車生產企業,年利潤![]() (出廠價
(出廠價![]() 投入成本)
投入成本)![]() 年銷售量.已知上年度生產電動小汽車的投入成本為
年銷售量.已知上年度生產電動小汽車的投入成本為![]() 萬元/輛,出廠價為
萬元/輛,出廠價為![]() 萬/輛,年銷售量為
萬/輛,年銷售量為![]() 輛,本年度為打造綠色環保電動小汽車,提高產品檔次,計劃增加投入成本,若每輛電動小汽車投入成本增加的比例為
輛,本年度為打造綠色環保電動小汽車,提高產品檔次,計劃增加投入成本,若每輛電動小汽車投入成本增加的比例為![]() (
(![]() ),則出廠價相應提高的比例為
),則出廠價相應提高的比例為![]() .同時年銷售量增加的比例為
.同時年銷售量增加的比例為![]() .
.
(1)寫出本年度預計的年利潤![]() (萬元)與投入成本增加的比例
(萬元)與投入成本增加的比例![]() 的函數關系式;
的函數關系式;
(2)為了使本年度的年利潤最大,每輛車投入成本增加的比例應為多少?最大年利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sinωx·cosωx-cos2ωx(ω>0)的最小正周期為
sinωx·cosωx-cos2ωx(ω>0)的最小正周期為![]() .
.
(1)求ω的值;
(2)在△ABC中,sinB,sinA,sinC成等比數列,求此時f(A)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2sin(x-![]() )-
)-![]() ,現將f(x)的圖象向左平移
,現將f(x)的圖象向左平移![]() 個單位長度,再向上平移
個單位長度,再向上平移![]() 個單位長度,得到函數g(x)的圖象.
個單位長度,得到函數g(x)的圖象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分別是△ABC三個內角A,B,C的對邊,a+c=4,且當x=B時,g(x)取得最大值,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①點P(-1,4)到直線3x+4y =2的距離為3.
②過點M(-3,5)且在兩坐標軸上的截距互為相反數的直線方程為![]() .
.
③命題“x∈R,使得x2﹣2x+1<0”的否定是真命題;
④“x ≤1,且y≤1”是“x + y ≤2”的充要條件.
其中不正確命題的序號是 _______________ .(把你認為不正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批零件共160個,其中一級品有48人,二級品有64個,三級品有32個,等外品有16個.從中抽取一個容量為20的樣本.試簡要敘述用簡單隨機抽樣、系統抽樣、分層抽樣法進行抽樣都是等可能抽樣.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】調查在![]() 級風的海上航行中71名乘客的暈船情況,在男人中有12人暈船,25人不暈船,在女人中有10人暈船,24人不暈船
級風的海上航行中71名乘客的暈船情況,在男人中有12人暈船,25人不暈船,在女人中有10人暈船,24人不暈船
(1)作出性別與暈船關系的列聯表;
(2)根據此資料,能否在犯錯誤的概率不超過0.1的前提下認為![]() 級風的海上航行中暈船與性別有關?
級風的海上航行中暈船與性別有關?
暈船 | 不暈船 | 總計 | |
男人 | |||
女人 | |||
總計 |
附:.![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com