
【題目】設關于x的一元二次方程![]() ,其中a,b是某范圍內的隨機數,分別在下列條件下,求上述方程有實根的概率.
,其中a,b是某范圍內的隨機數,分別在下列條件下,求上述方程有實根的概率.
(1)若隨機數a,b∈{1,2,3,4,5,6};
(2)若a是從區間[0,5]中任取的一個數,b是從區間[2,4]中任取的一個數.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)設事件A為“方程x2+2ax+b2=0有實根”,當a≥0,b≥0時,方程x2+2ax+b2=0有實根的充要條件為a≥b,利用列舉法能求出事件A發生的概率為P(A).
(2)試驗的全部結果所構成的區域為{(a,b)|0≤a≤5,2≤b≤4}.構成事件A的區域為{(a,b)|0≤a≤5,2≤b≤4,a≥b},數形結合能求出所求的概率.
設事件A為方程![]() 有實根,
有實根,
當![]() ,
,![]() 時,方程
時,方程![]() 有實根的充要條件為
有實根的充要條件為![]() .
.
基本事件共有36個:(1,1),(1,2),(1,3),(1,4)(1,5),(1,6),(2,1),(2,2),(2,3),(2,4)(2,5),(2,6),(3,1)(3,2),(3,3),(3,4),(3,5),(3,6),(4,1)(4,2)(4,3)(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4)(6,5),(6,6),其中第一個數表示a的取值,第二個數表示b的取值.事件A中包含21個基本事件,
故事件A發生的概率為![]() 。
。
(2) 試驗的全部結果所構成的區域為{(a,b)|0≤a≤5,2≤b≤4}.
構成事件A的區域為{(a,b)|0≤a≤5,2≤b≤4,a≥b},概率為兩者的面積之比,
所以所求的概率為P(A)=![]() 。
。


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
【題目】如圖:三棱錐P﹣ABC中,PA⊥底面ABC,若底面ABC是邊長為2的正三角形,且PB與底面ABC所成的角為 ![]() .若M是BC的中點,求:
.若M是BC的中點,求: 
(1)三棱錐P﹣ABC的體積;
(2)異面直線PM與AC所成角的大小(結果用反三角函數值表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,且
為直角梯形,且![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 為
為![]() 的中點,
的中點, ![]() 是棱
是棱![]() 的中點,
的中點, ![]() ,
,![]() .
.


(1)求證:![]() 平面BDM; (2)D到面PBC距離;
平面BDM; (2)D到面PBC距離;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在鈍角△ABC中,∠A為鈍角,令 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若
,若 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R).現給出下面結論:
(x,y∈R).現給出下面結論:
①當x= ![]() 時,點D是△ABC的重心;
時,點D是△ABC的重心;
②記△ABD,△ACD的面積分別為S△ABD , S△ACD , 當x= ![]() 時,
時, ![]() ;
;
③若點D在△ABC內部(不含邊界),則 ![]() 的取值范圍是
的取值范圍是 ![]() ;
;
④若 ![]() =λ
=λ ![]() ,其中點E在直線BC上,則當x=4,y=3時,λ=5.
,其中點E在直線BC上,則當x=4,y=3時,λ=5.
其中正確的有(寫出所有正確結論的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在定義域[﹣1,1]是奇函數,當x∈[﹣1,0]時,f(x)=﹣3x2 .
(1)當x∈[0,1],求f(x);
(2)對任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣1|.
(1)若不等式f(x+ ![]() )≥2m+1(m>0)的解集為(﹣∞,﹣2]∪[2,+∞),求實數m的值;
)≥2m+1(m>0)的解集為(﹣∞,﹣2]∪[2,+∞),求實數m的值;
(2)若不等式f(x)≤2y+ ![]() +|2x+3|,對任意的實數x,y∈R恒成立,求實數a的最小值.
+|2x+3|,對任意的實數x,y∈R恒成立,求實數a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
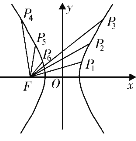
【題目】如圖所示,F為雙曲線C:![]() ﹣
﹣![]() =1的左焦點,雙曲線C上的點Pi與P7﹣i(i=1,2,3)關于y軸對稱,則|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦點,雙曲線C上的點Pi與P7﹣i(i=1,2,3)關于y軸對稱,則|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
A. 9 B. 16 C. 18 D. 27
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com