
設函數 的定義域為R,若存在常數M>0,使
的定義域為R,若存在常數M>0,使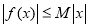 對 一切實數x均成 立,則稱
對 一切實數x均成 立,則稱 為“倍約束函數”,現給出下列函數:①
為“倍約束函數”,現給出下列函數:①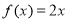 :②
:② :③
:③ ;④
;④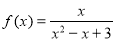 ⑤
⑤ 是定義在實數集R上的奇函數,且
是定義在實數集R上的奇函數,且
對一切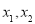 均有
均有 ,其中是“倍約束函數”的有( )
,其中是“倍約束函數”的有( )
A.1個 B.2個 C..3個 D.4個
C
【解析】
試題分析:【解析】
①對于函數 ,存在
,存在 ,使
,使 對 一切實數x均成 立,所以該函數是“倍約束函數”;
對 一切實數x均成 立,所以該函數是“倍約束函數”;
②對于函數 ,當
,當 時,
時, ,故不存在常數M>0,使
,故不存在常數M>0,使 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
③對于函數 ,當
,當 時,
時, ,故不存在常數M>0,使
,故不存在常數M>0,使 對 一切實數x均成 立,所以該函數不是“倍約束函數”;
對 一切實數x均成 立,所以該函數不是“倍約束函數”;
④對于函數 ,因為當
,因為當 時,
時, ;
;
當 時,
時, ,所以存在常數
,所以存在常數 ,使
,使 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
⑤由題設 是定義在實數集R上的奇函數,
是定義在實數集R上的奇函數, ,所以在
,所以在 中令
中令 ,于是有
,于是有 ,即存在常數
,即存在常數 ,使
,使 對 一切實數x均成 立, 所以該函數是“倍約束函數”;
對 一切實數x均成 立, 所以該函數是“倍約束函數”;
綜上可知“倍約束函數”的有①④⑤共三個,所以應選C.
考點:1、新定義;2、賦值法;3、基本初等函數的性質.


科目:高中數學 來源:2013-2014學年天津市紅橋區高三第一次模擬考試文科數學試卷(解析版) 題型:解答題
己知a∈R,函數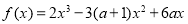
(1)若a=1,求曲線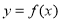 在點(2,f (2))處的切線方程;
在點(2,f (2))處的切線方程;
(2)若|a|>1,求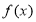 在閉區間[0,|2a|]上的最小值.
在閉區間[0,|2a|]上的最小值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河北區高三總復習質量檢測(一)文科數學試卷(解析版) 題型:解答題
如圖,在四棱錐P-ABCD中,側面PAD 底面ABCD,側棱
底面ABCD,側棱 ,底面ABCD為直角梯形,其中BC//AD,AB
,底面ABCD為直角梯形,其中BC//AD,AB AD,AD=2,AB=BC=l,E為AD中點.
AD,AD=2,AB=BC=l,E為AD中點.
(1)求證:PE 平面ABCD:
平面ABCD:
(2)求異面直線PB與CD所成角的余弦值:
(3)求點A到平面PCD的距離.

查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模試卷理科數學試卷(解析版) 題型:解答題
已知函數
(1)若函數 的圖象切x軸于點(2,0),求a、b的值;
的圖象切x軸于點(2,0),求a、b的值;
(2)設函數 的圖象上任意一點的切線斜率為k,試求
的圖象上任意一點的切線斜率為k,試求 的充要條件;
的充要條件;
(3)若函數 的圖象上任意不同的兩點的連線的斜率小于l,求證
的圖象上任意不同的兩點的連線的斜率小于l,求證 .
.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模試卷文科數學試卷(解析版) 題型:解答題
甲、乙兩人各擲一次骰子(均勻的正方體,六個面上分別為1,2,3,4,5,6點),所得點數分別為x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市河東區高三一模理科數學試卷(解析版) 題型:解答題
給定橢圓 .稱圓心在原點O,半徑為
.稱圓心在原點O,半徑為 的圓是橢圓C的“準圓”.若橢圓C的一個焦點為
的圓是橢圓C的“準圓”.若橢圓C的一個焦點為 ,其短軸上的一個端點到F的距離為
,其短軸上的一個端點到F的距離為 .
.
(1)求橢圓C的方程和其“準圓”方程;
(2)點P是橢圓C的“準圓”上的一個動點,過動點P作直線 ,使得
,使得 與橢圓C都只有一個交點,試判斷
與橢圓C都只有一個交點,試判斷 是否垂直?并說明理由.
是否垂直?并說明理由.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年天津市南開區高三第一次模擬考試理科數學試卷(解析版) 題型:填空題
如圖,平行四邊形ABCD的兩條對角線相交于點M,點P是MD的中點.若 =2,
=2, =1,且
=1,且 BAD=60o,則
BAD=60o,則  。
。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com