Question

天水市第一次聯考后，某校對甲、乙兩個文科班的數學考試成績進行分析，

規定：大于或等于120分為優秀，120分以下為非優秀．統計成績后，

得到如下的列聯表，且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為.

	優秀	非優秀	合計
甲班	10
乙班		30
合計			110

（1）請完成上面的列聯表；

（2）根據列聯表的數據，若按99.9%的可靠性要求，能否認為“成績與班級有關系”；

（3）若按下面的方法從甲班優秀的學生中抽取一人：把甲班優秀的10名學生從2到11進行編號，先后兩次拋擲一枚均勻的骰子，出現的點數之和為被抽取人的序號。試求抽到9號或10號的概率。

參考公式與臨界值表：。

	0.100	0.050	0.025	0.010	0.001
	2.706	3.841	5.024	6.635	10.828

 

 

Answer 1

【答案】

（1）

	優秀	非優秀	合計
甲班	10	50	60
乙班	20	30	50
合計	30	80	110

 

（2）計算得到K²= ≈7.487＜10.828．因此按99.9%的可靠性要求，不能認為“成績與班級有關系”

（3）抽到9號或10號的概率為．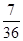

【解析】

試題分析：

思路分析：此類問題（1）（2）直接套用公式，經過計算“卡方”，與數表對比，作出結論。（3）是典型的古典概型概率的計算問題，確定兩個“事件”數，確定其比值。

解：（1）               4分

	優秀	非優秀	合計
甲班	10	50	60
乙班	20	30	50
合計	30	80	110

（2）根據列聯表中的數據，得到K²= ≈7.487＜10.828．因此按99.9%的

可靠性要求，不能認為“成績與班級有關系”           8分

（3）設“抽到9或10號”為事件A，先后兩次拋擲一枚均勻的骰子，出現的點數為（x，y）．所有的基本事件有：（1，1）、（1，2）、（1，3）、…、（6，6）共36個．事件A包含的基本事件有：（3，6）、（4，5）、（5，4）、（6，3）、（5，5）、（4，6）（6，4）共7個．所以P(A)= 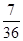，即抽到9號或10號的概率為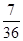．      12分

考點：“卡方檢驗”，古典概型概率的計算。

點評：中檔題，獨立性檢驗問題，主要是通過計算“卡方”，對比數表，得出結論。古典概型概率的計算中，常用“樹圖法”或“坐標法”確定事件數，以防重復或遺漏。