例
（2005高考福建卷）已知函數
的圖象過點P（0，2），且在點M（－1，f（－1））處的切線方程為
. （Ⅰ）求函數
的解析式；
【思維分析】利用導數的幾何意義解答。
解析：（Ⅰ）由
的圖象經過P（0，2），知d=2，所以
由在
處的切線方程是，知
故所求的解析式是
【知識點歸類點拔】導數的幾何意義:函數y=f(x)在點
處的導數，就是曲線y=(x)在點
處的切線的斜率．由此，可以利用導數求曲線的切線方程．具體求法分兩步： (1)求出函數y=f(x)在點處的導數，即曲線y=f(x)在點處的切線的斜率；(2)在已知切點坐標和切線斜率的條件下，求得切線方程為 
特別地，如果曲線y=f(x)在點處的切線平行于y軸，這時導數不存，根據切線定義，可得切線方程為
。利用導數的幾何意義作為解題工具，有可能出現在解析幾何綜合試題中，復習時要注意到這一點.
科目：高中數學 來源： 題型：
【練】
（1）（2005高考北京卷）已知函數f(x)=－x3＋3x2＋9x＋a, （I）求f(x)的單調遞減區間；（II）若f(x)在區間[－2，2]上的最大值為20，求它在該區間上的最小值．答案：（1）（－∞，－1），（3，＋∞）（2）－7
查看答案和解析>>
科目：高中數學 來源：2012年人教A版高中數學必修三2.2用樣本估計總體練習卷（一）（解析版） 題型：選擇題
(2009年高考福建卷)一個容量為100的樣本，其數據的分組與各組的頻數如下：
|
組別 |
(0,10] |
(10,20] |
(20,30] |
(30,40] |
(40,50] |
(50,60] |
(60,70] |
|
頻數 |
12 |
13 |
24 |
15 |
16 |
13 |
7 |
則樣本數據落在(10,40]上的頻率為( )
A．0.13 B．0.39
C．0.52 D．0.64
查看答案和解析>>
科目：高中數學 來源：2012年人教A版高中數學必修一3.1函數與方程練習卷（一）（解析版） 題型：選擇題
(2010年高考福建卷)函數f(x)＝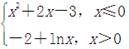
的零點個數為( )
A．0 B．1
C．2 D．3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，點P（
，0）是函數
的圖象的一個公共點，兩函數的圖象在點P處有相同的切線.（Ⅰ）用