【題目】已知
，函數
.
（1）當
時，求函數
的單調遞增區間；
（2）求函數
的零點個數.
【答案】（1）見解析；（2）見解析
【解析】
(1)先根據絕對值定義化為分段函數形式，再分別根據二次函數性質確定單調遞增區間，(2)作函數
圖象，根據圖象分類討論零點個數.
（1）當
時，
當
時，
，的對稱軸為
所以，的單調遞增區間為
當
時，
，的對稱軸為
所以，的單調遞增區間為
（2）令
，即
，
,
求函數
的零點個數，即求
與
的交點個數；
當
時，
，的對稱軸為
當
時，
，的對稱軸為
①當
時，
，
故由圖像可得，
與只存在一個交點.
②當
時，
，且
，
故由圖像可得，
當時，
，
與只存在兩個交點；
當
時，
，與只存在一個交點；
當
時，
，與只存在三個交點.
③當
時， 
，
故由圖像可得，與只存在一個交點.
綜上所述：當時，
存在三個零點；
當時，存在兩個零點；
當
時，存在一個零點.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】某市政府為了引導居民合理用水，決定全面實施階梯水價，階梯水價原則上以住宅（一套住宅為一戶）的月用水量為基準定價：若用水量不超過12噸時，按4元/噸計算水費；若用水量超過12噸且不超過14噸時，超過12噸部分按6.60元/噸計算水費；若用水量超過14噸時，超過14噸部分按7.80元/噸計算水費．為了了解全市居民月用水量的分布情況，通過抽樣，獲得了100戶居民的月用水量（單位：噸），將數據按照[0，2]，（2，4]，…，（14，16]分成8組，制成了如圖1所示的頻率分布直方圖． 
（Ⅰ）假設用抽到的100戶居民月用水量作為樣本估計全市的居民用水情況．
（ i）現從全市居民中依次隨機抽取5戶，求這5戶居民恰好3戶居民的月用水用量都超過12噸的概率；
（ⅱ）試估計全市居民用水價格的期望（精確到0.01）；
（Ⅱ）如圖2是該市居民李某2016年1～6月份的月用水費y（元）與月份x的散點圖，其擬合的線性回歸方程是 
．若李某2016年1～7月份水費總支出為294.6元，試估計李某7月份的用水噸數．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直三棱柱ABC﹣A1B1C1中，∠ABC=120°，AB=2，BC=CC1=1，則異面直線AB1與BC1所成角的余弦值為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平行六面體ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1= 
，∠BAD=120°．
（Ⅰ）求異面直線A1B與AC1所成角的余弦值；
（Ⅱ）求二面角B﹣A1D﹣A的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，PA⊥底面ABC，∠BAC=90°．點D，E，N分別為棱PA，PC，BC的中點，M是線段AD的中點，PA=AC=4，AB=2．
（Ⅰ）求證：MN∥平面BDE；
（Ⅱ）求二面角C﹣EM﹣N的正弦值；
（Ⅲ）已知點H在棱PA上，且直線NH與直線BE所成角的余弦值為 
，求線段AH的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，
，
，
以AC的中點O為球心，AC為直徑的球面交PD于點M，交PC于點N.
（1）求證：平面ABM⊥平面PCD；
（2）求直線CD與平面ACM所成角的大小；
（3）求點N到平面ACM的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
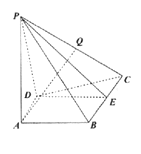
【題目】如圖，在四棱錐
中，
平面
，在直角梯形中，
，
，
，
為線段
的中點
（1）求證：平面
平面
（2）在線段
上是否存在點
，使得
平面
?若存在，求出點 的位置；若不存在，請說明理由
（3）若
是
中點，
，
，
，求三棱錐
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
