桃江四中假期后勤維修的一項工作是請30名木工制作200把椅子和100張課桌,已知一名工人在單位時間內可以制作10把椅子或7張課桌,將這30名工人分成兩組,一組制作課桌,一組制作椅子,兩組同時開工.設制作課桌的人數為x.
(1).分別用含x的式子表示制作200把椅子的單位時間t1和100張課桌的單位時間t2
(2).當x為何值時,完成此項工作的時間T最短?
解:(1)由題中一名工人在單位時間內可制作10把椅子或7張課桌,制作課桌的人數為x名,則制作椅子的工人有30-x名,
則200把椅子的單位時間t
1=
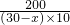
=
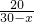
(1≤x≤29).
制作100張課桌所用的時間為
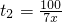
(1≤x≤29).
(2)令T=
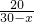
-
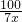
當|T|值最小時,表示工人分別完成兩項工作的時間最接近,
此時完成此項工作時間最短,
當x=12時,T=-
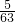
,當x=13時,T=
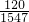
即當x=13時,完成此項工作時間最短.
分析:(1)由已知制作課桌的人數為x名,我們可得制作椅子的工人有30-x名,又由已知中一名工人在單位時間內可制作10把椅子或7張課桌.共需要制作200把椅子和100張課桌,進而可以得到制作200把椅子和100張課桌所用的時間;
(2)令T=t
1-t
2,當|T|值最小時,表示工人分別完成兩項工作的時間最接近,此時完成此項工作時間最短.
點評:本題考查的知識點是函數模型的選擇與應用,函數最小值的意義,其中(1)的關鍵是根據已知,分別確定制作燈籠和展板的工作量,及工作效率,(2)的關鍵是正確理解完成此項工作時間最短含義.

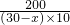 =
=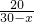 (1≤x≤29).
(1≤x≤29).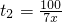 (1≤x≤29).
(1≤x≤29).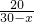 -
-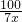
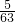 ,當x=13時,T=
,當x=13時,T=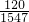


 名校課堂系列答案
名校課堂系列答案