
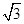 ,求l的方程;
,求l的方程;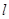 的方程為:
的方程為: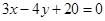 或
或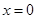 (2)
(2)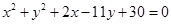
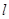 的距離為2 當直線的斜率存在時,設所求直線
的距離為2 當直線的斜率存在時,設所求直線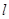 的方程為:
的方程為: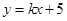 即
即 由點到直線的距離公式即可求出k的值,從而得直線
由點到直線的距離公式即可求出k的值,從而得直線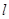 的方程 然后再考慮斜率不存在時的情況 (2)設過點P的圓C的弦的中點為
的方程 然后再考慮斜率不存在時的情況 (2)設過點P的圓C的弦的中點為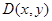 ,則
,則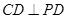 即
即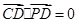 由此等式即可得中點D的軌跡方程 這屬于利用等量關系求軌跡方程的問題
由此等式即可得中點D的軌跡方程 這屬于利用等量關系求軌跡方程的問題 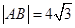 ,設
,設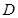 是線段
是線段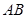 的中點,則
的中點,則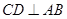
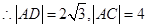 點C的坐標為(-2,6) 在
點C的坐標為(-2,6) 在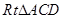 中,可得
中,可得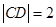
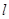 的方程為:
的方程為: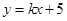 即
即
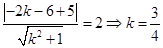
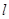 的方程為:
的方程為: 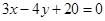 4分
4分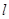 的斜率不存在時,也滿足題意,此時方程為:
的斜率不存在時,也滿足題意,此時方程為: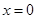
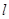 的方程為:
的方程為: 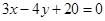 或
或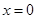 6分
6分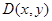 ,則
,則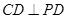 即
即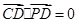
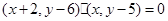 化簡得所求軌跡的方程為:
化簡得所求軌跡的方程為: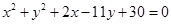 12分
12分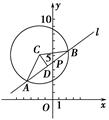


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com