【答案】
分析:(1)利用導數的幾何意義即可得出切線的斜率f
′(1),再利用點斜式即可得到切線的方程;
(2)利用導數得到g(x)的極小值即最小值,g(x)=m有零點?m≥g(x)
min;
(3)令h(x)=g(x)-f(x),利用導數得出其最小值,g(x)-f(x)=0有兩個相異實根?h(x)
min<0.
解答:解:(1)∵f
′(x)=-2x+2,∴f
′(1)=0.
而f(1)=-1+2+t-1=t,
∴過點(1,f(1))與y=f(x)圖象相切的直線方程是y-t=0.
(2)由
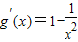
=

,x>0,令g
′(x)=0,解得x=1.
解g
′(x)>0,得x>1,可得g(x)在(1,+∞)上單調遞增;解g
′(x)<0,得0<x<1,可得g(x)在(0,1)上單調遞減.
因此當x=1時,g(x)取得極小值即最小值,g(1)=2,
∵g(x)=m有零點,∴m的取值范圍是[2,+∞);
(3)令h(x)=g(x)-f(x)=
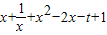
=
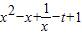
(x>0),
則
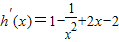
=
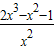
=
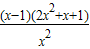
,
令h
′(x)=0,解得x=1.
解h
′(x)>0,得x>1,可得h(x)在(1,+∞)上單調遞增;解h
′(x)<0,得0<x<1,可得h(x)在(0,1)上單調遞減.
因此當x=1時,函數h(x)取得最小值,h(1)=2-t,
又x→0
+時,h(x)→+∞;當x→+∞時,h(x)→+∞.
因此當h(1)<0,即t>2時,h(x)在x>0時與x軸由兩個交點,即g(x)-f(x)=0有兩個相異實根.
點評:本題考查了利用導數研究函數的單調性、極值與最值、導數的幾何意義、函數的零點與方程的根等價轉化等基礎知識與基本技能,考查了推理能力和計算能力.

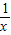 .
.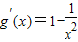 =
= ,x>0,令g′(x)=0,解得x=1.
,x>0,令g′(x)=0,解得x=1.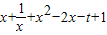 =
=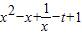 (x>0),
(x>0),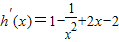 =
=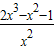 =
=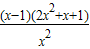 ,
,

 出彩同步大試卷系列答案
出彩同步大試卷系列答案