
 .
.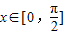 時,求f(x)的值域.
時,求f(x)的值域.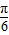 +2x)+2,從而求出函數(shù)的最小正周期,再令2kπ-
+2x)+2,從而求出函數(shù)的最小正周期,再令2kπ-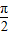 ≤
≤ +2x≤2kπ+
+2x≤2kπ+ ,k∈z,求出x的范圍,即可求得函數(shù)的單調(diào)增區(qū)間.
,k∈z,求出x的范圍,即可求得函數(shù)的單調(diào)增區(qū)間. 時,求出
時,求出 +2x的范圍,可得sin(
+2x的范圍,可得sin( +2x) 的范圍,從而求得2sin(
+2x) 的范圍,從而求得2sin( +2x)+2的范圍,即為所求.
+2x)+2的范圍,即為所求. =cos2x+
=cos2x+ sin2x+2
sin2x+2 +2x)+2,
+2x)+2, =π.
=π. ≤
≤ +2x≤2kπ+
+2x≤2kπ+ ,k∈z,可得kπ-
,k∈z,可得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈z,
,k∈z, .
. 時,
時, +2x∈[
+2x∈[ ,
, ],sin(
],sin(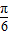 +2x)∈[-
+2x)∈[- ,1],
,1],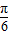 +2x)+2∈[1,4],
+2x)+2∈[1,4],

科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年山東省臨沂市臨沭縣高三(上)期中數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年北京市十一學(xué)校高三(上)第五次月考數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
 .
. 個單位,得到函數(shù)g(x)的圖象,求函數(shù)g(x)在區(qū)間[0,π]上的最大值和最小值.
個單位,得到函數(shù)g(x)的圖象,求函數(shù)g(x)在區(qū)間[0,π]上的最大值和最小值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年湖南省衡陽八中高一(上)期中數(shù)學(xué)試卷(解析版) 題型:解答題
 .
. 上恒成立,求實數(shù)m的取值范圍.
上恒成立,求實數(shù)m的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年山東省濰坊市高三(上)12月統(tǒng)考數(shù)學(xué)試卷(解析版) 題型:解答題
 .
. 成等差數(shù)列,且
成等差數(shù)列,且 =9,求a的值.
=9,求a的值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2008-2009學(xué)年湖北省部分重點中學(xué)聯(lián)考高三(上)期中數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
 .
.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com