
【題目】某校從參加高一年級期末考試的學生中抽出60名學生,將其數(shù)學成績(均為整數(shù))分成六段![]() ,
, ![]() …
…![]() 后,畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
后,畫出如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
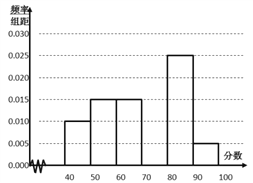
(1)求第四小組的頻率,補全頻率分布直方圖,并估計該校學生的數(shù)學成績的中位數(shù).
(2)從被抽取的數(shù)學成績是![]() 分以上(包括
分以上(包括![]() 分)的學生中選兩人,求他們在同一分數(shù)段的概率.
分)的學生中選兩人,求他們在同一分數(shù)段的概率.
(3)假設從全市參加高一年級期末考試的學生中,任意抽取![]() 個學生,設這四個學生中數(shù)學成績?yōu)?0分以上(包括
個學生,設這四個學生中數(shù)學成績?yōu)?0分以上(包括![]() 分)的人數(shù)為
分)的人數(shù)為![]() (以該校學生的成績的頻率估計概率),求
(以該校學生的成績的頻率估計概率),求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
【答案】(1)![]() 分.(2)
分.(2)![]() .(3)見解析.
.(3)見解析.
【解析】試題分析:⑴通過各組的頻率和等于![]() ,求出第四組的頻率,考查直方圖,求出中位數(shù)即可;
,求出第四組的頻率,考查直方圖,求出中位數(shù)即可; ![]() 分別求出
分別求出![]() ,
, ![]() ,
, ![]() 的人數(shù)是
的人數(shù)是![]() ,
, ![]() ,
, ![]() ,然后利用古典概型概率求解即可;⑶判斷概率類型
,然后利用古典概型概率求解即可;⑶判斷概率類型![]() ,即可寫出
,即可寫出![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望
解析:(1)因為各組的頻率和等于1,故第四組的頻率:
![]()
![]() .
.
直方圖如圖所示.
中位數(shù)是![]() ,
,
估計這次考試的中位數(shù)是![]() 分.
分.

(2)![]() ,
, ![]() ,
, ![]() 的人數(shù)是
的人數(shù)是![]() ,
, ![]() ,
, ![]() ,所以從成績是
,所以從成績是![]() 分以上(包括
分以上(包括![]() 分)的學生中選兩人,他們在同一分數(shù)段的概率:
分)的學生中選兩人,他們在同一分數(shù)段的概率:
![]() .
.
(3)因為![]() ,
, ![]() ,
, ![]() ,
,
所以其分布列為:
| 0 | 1 | 2 | 3 | 4 |
| 0.2401 | 0.4116 | 0.2646 | 0.0756 | 0.0081 |
數(shù)學期望為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】設集合![]() ,集合
,集合![]() .
.
(1)若“![]() ”是“
”是“![]() ”的必要條件,求實數(shù)
”的必要條件,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() 中只有一個整數(shù),求實數(shù)
中只有一個整數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
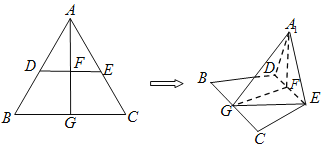
【題目】邊長為2的正三角形ABC中,點D,E,G分別是邊AB,AC,BC的中點,連接DE,連接AG交DE于點![]() 現(xiàn)將
現(xiàn)將![]() 沿DE折疊至
沿DE折疊至![]() 的位置,使得平面
的位置,使得平面![]() 平面BCED,連接A1G,EG.
平面BCED,連接A1G,EG.
![]() 證明:DE∥平面A1BC
證明:DE∥平面A1BC
![]() 求點B到平面A1EG的距離.
求點B到平面A1EG的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】【選修4-4:坐標系與參數(shù)方程】
極坐標系的極點為直角坐標系![]() 的原點,極軸為
的原點,極軸為![]() 軸的正半軸,兩神坐標系中的長度單位相同.已知曲線
軸的正半軸,兩神坐標系中的長度單位相同.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,
, ![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)在曲線![]() 上求一點,使它到直線
上求一點,使它到直線![]() :
: 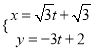 (
(![]() 為參數(shù))的距離最短,寫出
為參數(shù))的距離最短,寫出![]() 點的直角坐標.
點的直角坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題p:函數(shù)f(x)=x2-2mx+4在[2,+∞)上單調(diào)遞增,命題q:關于x的不等式mx2+4(m-2)x+4>0的解集為R.若p∨q為真命題,p∧q為假命題,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,某小區(qū)中央廣場由兩部分組成,一部分是邊長為![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 為直徑的半圓,其圓心為
為直徑的半圓,其圓心為![]() .規(guī)劃修建的
.規(guī)劃修建的![]() 條直道
條直道![]() ,
, ![]() ,
, ![]() 將廣場分割為
將廣場分割為![]() 個區(qū)域:Ⅰ、Ⅲ、Ⅴ為綠化區(qū)域(圖中陰影部分),Ⅱ、Ⅳ、Ⅵ為休閑區(qū)域,其中點
個區(qū)域:Ⅰ、Ⅲ、Ⅴ為綠化區(qū)域(圖中陰影部分),Ⅱ、Ⅳ、Ⅵ為休閑區(qū)域,其中點![]() 在半圓弧上,
在半圓弧上, ![]() 分別與
分別與![]() ,
, ![]() 相交于點
相交于點![]() ,
, ![]() .(道路寬度忽略不計)
.(道路寬度忽略不計)
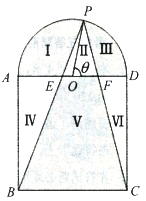
(1)若![]() 經(jīng)過圓心,求點
經(jīng)過圓心,求點![]() 到
到![]() 的距離;
的距離;
(2)設![]() ,
, ![]() .
.
①試用![]() 表示
表示![]() 的長度;
的長度;
②當![]() 為何值時,綠化區(qū)域面積之和最大.
為何值時,綠化區(qū)域面積之和最大.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com