

 BD2,接著由AB,AD及cosA的值,利用余弦定理表示出BD2,可表示出三角形BCD的面積,兩者相加去括號后,利用兩角和與差的正弦函數公式化簡可表示出四邊形ABCD的面積,并求出此時θ的范圍;
BD2,接著由AB,AD及cosA的值,利用余弦定理表示出BD2,可表示出三角形BCD的面積,兩者相加去括號后,利用兩角和與差的正弦函數公式化簡可表示出四邊形ABCD的面積,并求出此時θ的范圍; 的范圍,再由正弦函數的圖象與性質可得出面積S的最大值,以及此時θ的度數.
的范圍,再由正弦函數的圖象與性質可得出面積S的最大值,以及此時θ的度數. AB•AD•sinA=
AB•AD•sinA= ×1×1×sinθ=
×1×1×sinθ= sinθ,
sinθ, BD2,
BD2, sinθ+
sinθ+ (2-2cosθ),
(2-2cosθ), +sin(θ-
+sin(θ- )其中0<θ<π;
)其中0<θ<π; +sin(θ-
+sin(θ- ),
), <θ-
<θ- <
< ,
, =
= 時,S取得最大值1+
時,S取得最大值1+ ,此時θ=
,此時θ= +
+ =
= .
.

 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:
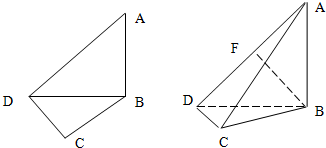 如圖,在平面四邊形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,現將四邊形ABCD沿BD折起,使平面ABD⊥平面BDC,設點F為棱AD的中點.
如圖,在平面四邊形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,現將四邊形ABCD沿BD折起,使平面ABD⊥平面BDC,設點F為棱AD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
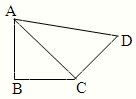 如圖,在平面四邊形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿對角線AC將此四邊形折成直二面角.
如圖,在平面四邊形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿對角線AC將此四邊形折成直二面角.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
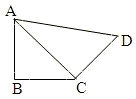 如圖,在平面四邊形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿對角線AC將此四邊形折成直二面角.
如圖,在平面四邊形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿對角線AC將此四邊形折成直二面角.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com