
【題目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,寫出
,寫出![]() 的單調區間:
的單調區間:
(2)若函數![]() 恰有三個不同的零點,且這些零點之和為-2,求a、b的值;
恰有三個不同的零點,且這些零點之和為-2,求a、b的值;
(3)若函數![]() 在
在![]() 上有四個不同零點
上有四個不同零點![]() ,求
,求![]() 的最大值。
的最大值。
【答案】(1)![]() 遞減,
遞減,![]() 遞增;(2)
遞增;(2)![]() ;(3)4
;(3)4
【解析】
(1)由![]() ,得出函數的解析式
,得出函數的解析式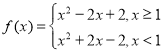 ,再做出圖像可得函數
,再做出圖像可得函數![]() 的單調區間;
的單調區間;
(2)令![]() ,即
,即![]() 或
或![]() ,再由
,再由![]() ,可得方程
,可得方程![]() 中有兩個不等的實根,要使函數
中有兩個不等的實根,要使函數![]() 恰有三個不同的零點,且這些零點之和為-2,,則需方程
恰有三個不同的零點,且這些零點之和為-2,,則需方程![]() 有兩個相等的實根,可建立關于的方程,解之可得
有兩個相等的實根,可建立關于的方程,解之可得![]() 的值;
的值;
(3)由![]() ,即
,即![]() 或
或![]() ,設
,設![]() 的兩根為
的兩根為![]() ,并且可得
,并且可得![]() ,
,![]() 的兩根為
的兩根為![]() ,并且可得
,并且可得![]() ,所以
,所以![]() 兩根中一正一負,再由
兩根中一正一負,再由![]() 均在
均在![]() 內,得
內,得![]() 的負根
的負根![]() ,從而可得
,從而可得![]() 的最大值.
的最大值.
(1)當![]() 時,
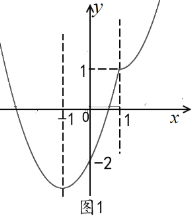
時,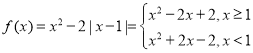 ,做出圖像如下圖1所示,
,做出圖像如下圖1所示,
所以![]() 的單調區間是:在
的單調區間是:在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
(2)令![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() ,
,
整理得![]() 或
或![]() ,
,
因為![]() ,所以方程
,所以方程![]() 中
中![]() 恒成立,也即是
恒成立,也即是![]() 一定有兩個不等的實根,
一定有兩個不等的實根,
設這兩個實根為![]() 并且
并且![]() ,要使函數
,要使函數![]() 恰有三個不同的零點,且這些零點之和為-2,
恰有三個不同的零點,且這些零點之和為-2,
現需方程![]() 有兩個相等的實根,設此根為
有兩個相等的實根,設此根為![]() ,且
,且![]() ,
,
所以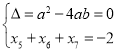 ,即
,即 ,解得
,解得![]() ,
,
所以![]() 的值為
的值為![]() ;
;
(3)若![]() ,即
,即![]() 或
或![]() ,
,
設![]() 的兩根為
的兩根為![]() ,則
,則![]() ,
,
![]() 的兩根為
的兩根為![]() ,則
,則![]() ,所以
,所以![]() 兩根中一正一負,
兩根中一正一負,
![]() ,
,
![]() 均在
均在![]() 內,
內,![]() 的負根
的負根![]() 在
在![]() 內,
內,
![]() ,
,![]() ,
,
所以![]() 的最大值為4.
的最大值為4.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 的圖像經過變換
的圖像經過變換![]() 后所得的圖像對應的函數與
后所得的圖像對應的函數與![]() 的值域相同,則稱變換
的值域相同,則稱變換![]() 是
是![]() 的同值變換,下面給出了四個函數與對應的變換:
的同值變換,下面給出了四個函數與對應的變換:
①![]() 將函數
將函數![]() 的圖像關于
的圖像關于![]() 軸作對稱變換;
軸作對稱變換;
②![]() 將函數
將函數![]() 的圖像關于
的圖像關于![]() 軸作對稱變換;
軸作對稱變換;
③![]() 將函數
將函數![]() 的圖像關于點(-1,1)作對稱變換;
的圖像關于點(-1,1)作對稱變換;
④![]() 將函數
將函數![]() 的圖像關于點(-1,0)作對稱變換;
的圖像關于點(-1,0)作對稱變換;
其中![]() 是
是![]() 的同值變換的有_______.(寫出所有符合題意的序號)
的同值變換的有_______.(寫出所有符合題意的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義運算“![]() ”:對于任意
”:對于任意![]() ,
,![]() (等式的右邊是通常的加減乘運算).若數列
(等式的右邊是通常的加減乘運算).若數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() 對任意
對任意![]() 都成立.
都成立.
(1)求![]() 的值,并推導出用
的值,并推導出用![]() 表示
表示![]() 的解析式;
的解析式;
(2)若![]() ,令
,令![]() ,證明數列
,證明數列![]() 是等差數列;
是等差數列;
(3)若![]() ,令
,令![]() ,數列
,數列![]() 滿足
滿足![]() ,求正實數b的取值范圍.
,求正實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術·均輸》中有如下問題:“今有五人分十錢,令上二人所得與下三人等,問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分10錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列,問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,甲所得為( )
A.![]() 錢B.
錢B.![]() 錢C.
錢C.![]() 錢D.
錢D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 是定義在區間
是定義在區間![]() 上且同時滿足如下條件的函數
上且同時滿足如下條件的函數![]() 所組成的集合:
所組成的集合:
①對任意的![]() ,都有
,都有![]() ;
;
②存在常數![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]()
(1)設![]() ,試判斷
,試判斷![]() 是否屬于集合
是否屬于集合![]() ;
;
(2)若![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,求證:滿足條件的
,求證:滿足條件的![]() 是唯一的;
是唯一的;
(3)設![]() ,且
,且![]() ,試求參數
,試求參數![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列舉法表示集合C;
(2)設集合C的含n個元素所有子集為![]() ,記有限集合M的所有元素和為
,記有限集合M的所有元素和為![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的兩個不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合對![]() 的個數
的個數![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過多年的運作,“雙十一”搶購活動已經演變成為整個電商行業的大型集體促銷盛宴.為迎接2014年“雙十一”網購狂歡節,某廠家擬投入適當的廣告費,對網上所售產品進行促銷.經調查測算,該促銷產品在“雙十一”的銷售量p萬件與促銷費用x萬元滿足![]() (其中
(其中![]() ,a為正常數).已知生產該產品還需投入成本
,a為正常數).已知生產該產品還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為
![]() 元/件,假定廠家的生產能力完全能滿足市場的銷售需求.
元/件,假定廠家的生產能力完全能滿足市場的銷售需求.
(1)將該產品的利潤y萬元表示為促銷費用x萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中真命題的序號為(少填或錯填均不得分)______.若一個球的半徑縮小為原來的一半,則其體積縮小為原來的八分之一;②若兩組數據的平均值相等,則它們的標準差也相等;③直線![]() 與圓
與圓![]() 相切;④若兩個平面都垂直于同一個平面,則這兩個平面平行.
相切;④若兩個平面都垂直于同一個平面,則這兩個平面平行.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設計一個隨機試驗,使一個事件的概率與某個未知數有關,然后通過重復試驗,以頻率估計概率,即可求得未知數的近似解,這種隨機試驗在數學上稱為隨機模擬法,也稱為蒙特卡洛法。比如要計算一個正方形內部不規則圖形的面積,就可以利用撒豆子,計算出落在不規則圖形內部和正方形內部的豆子數比近似等于不規則圖形面積與正方形面積比,從而近似求出不規則圖形的面積.
統計學上還有一個非常著名的蒲豐投針實驗:平面上間隔![]() 的平行線,向平行線間的平面上任意投擲一枚長為
的平行線,向平行線間的平面上任意投擲一枚長為![]() 的針
的針![]() ,通過多次實驗可以近似求出針與任一平行線(以
,通過多次實驗可以近似求出針與任一平行線(以![]() 為例)相交(當針的中點在平行線外不算相交)的概率.以
為例)相交(當針的中點在平行線外不算相交)的概率.以![]() 表示針的中點與最近一條平行線
表示針的中點與最近一條平行線![]() 的距離,又以
的距離,又以![]() 表示
表示![]() 與
與![]() 所成夾角,如圖甲,易知滿足條件:
所成夾角,如圖甲,易知滿足條件:![]() ,
,![]() .
.
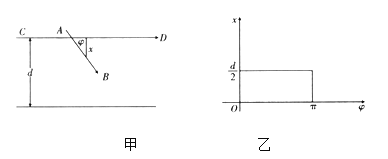
由這兩式可以確定平面上的一個矩形![]() ,如圖乙,在圖甲中,當
,如圖乙,在圖甲中,當![]() 滿足___________(
滿足___________(![]() 與
與![]() ,
,![]() 之間的關系)時,針與平行線相交(記為事件
之間的關系)時,針與平行線相交(記為事件![]() ).可用從實驗中獲得的頻率去近似
).可用從實驗中獲得的頻率去近似![]() ,即投針
,即投針![]() 次,其中相交的次數為
次,其中相交的次數為![]() ,則
,則![]() ,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,
,歷史上有一個數學家親自做了這實驗,他投擲的次數是5000,相交的次數為2550次,![]() ,
,![]() ,依據這個實驗求圓周率
,依據這個實驗求圓周率![]() 的近似值_________.(精確到3位小數)
的近似值_________.(精確到3位小數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com