
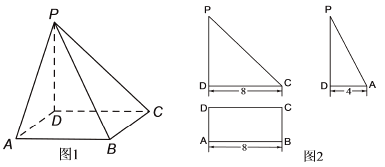
【題目】如圖1是四棱錐的直觀圖,其正(主)視圖和側(左)視圖均為直角三角形,俯視圖外框為矩形,相關數據如圖2所示.
(1)設![]() 中點為
中點為![]() ,在直線
,在直線![]() 上找一點
上找一點![]() ,使得
,使得![]() 平面
平面![]() ,并說明理由;
,并說明理由;
(2)若二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求四棱錐
,求四棱錐![]() 的外接球的表面積.
的外接球的表面積.
【答案】(1) 見解析;(2) ![]() .
.
【解析】試題分析:(1)利用中位線定理構造平行四邊形,得到![]() ;(2) 由二面角
;(2) 由二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,得到
,得到![]() ,明確外接球的直徑即為PB,易得四棱錐
,明確外接球的直徑即為PB,易得四棱錐![]() 的外接球的表面積.
的外接球的表面積.
試題解析:
(1)當![]() 是
是![]() 中點時,
中點時, ![]() 平面
平面![]() ,
,
證明如下:取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,
,
在![]() 中,
中, ![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,
∴![]() 是
是![]() 的中位線,
的中位線,
∴![]() 且
且![]() ,又
,又![]() 是
是![]() 中點,
中點, ![]() ,
,
∴![]() 且
且![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
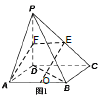
(2)由三視圖可得![]() 平面
平面![]() ,
,
在底面![]() 中,過
中,過![]() 作
作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
在底面矩形![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
在![]() 中,又
中,又![]() ,
,
∴![]() ,∴
,∴![]() .
.
由直觀圖易知四棱錐![]() 的外接球的直徑即為
的外接球的直徑即為![]() ,
,
∴![]() .
.
故四棱錐![]() 的外接球的表面積為
的外接球的表面積為![]() .
.


 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】現有一個質地均勻的正四面體骰子,每個面上分別標有數字1、2、3、4,將這個骰子連續投擲兩次,朝下一面的數字分別記為![]() ,試計算下列事件的概率:
,試計算下列事件的概率:
(1)事件![]() ;
;
(2)事件![]() :函數
:函數![]() 在區間
在區間![]() 上為增函數.
上為增函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義為![]() 的函數
的函數![]() 滿足下列條件:①對任意的實數
滿足下列條件:①對任意的實數![]() 都有:
都有:
![]() ;②當
;②當![]() 時,
時,![]() .
.
(1)求![]() ;
;
(2)求證:![]() 在
在![]() 上為增函數;
上為增函數;
(3)若![]() ,關于
,關于![]() 的不等式
的不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有![]() 、
、![]() 、
、![]() 三個工作點,需要建立一個公共無線網絡發射點
三個工作點,需要建立一個公共無線網絡發射點![]() ,使得發射點到三個工作點的距離相等.已知這三個工作點之間的距離分別為
,使得發射點到三個工作點的距離相等.已知這三個工作點之間的距離分別為![]()
![]() ,
,![]()
![]() ,
,![]()
![]() .假定
.假定![]() 、
、![]() 、
、![]() 、
、![]() 四點在同一平面內.
四點在同一平面內.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求點![]() 到直線
到直線![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,其中
,其中![]() 為實數.
為實數.
(1)是否存在![]() ,使得
,使得![]() ?若存在,求出實數
?若存在,求出實數![]() 的取值范圍;若不存在,請說明理由;
的取值范圍;若不存在,請說明理由;
(2)若集合![]() 中恰有5個元素,求實數
中恰有5個元素,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》是我國古代數學名著.在這部著作中,許多數學問題都是以歌訣形式呈現的,“竹筒容米”就是其中一首:家有八節竹一莖,為因盛米不均平;下頭三節三生九,上梢三節貯三升;唯有中間二節竹,要將米數次第盛;若是先生能算法,也教算得到天明!大意是:用一根8節長的竹子盛米,每節竹筒盛米的容積是不均勻的,下端3節可盛米3.9升,上端3節可盛米3升.要按依次盛米容積相差同一數量的方式盛米,中間兩節可盛米多少升?由以上條件,計算出這根八節竹筒的容積為( )
A. ![]() 升 B.
升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司有30名男職員和20名女職員,公司進行了一次全員參與的職業能力測試,現隨機詢問了該公司5名男職員和5名女職員在測試中的成績(滿分為30分),可知這5名男職員的測試成績分別為16,24,18,
22,20,5名女職員的測試成績分別為18,23,23,18,23,則下列說法一定正確的是( )
A. 這種抽樣方法是分層抽樣
B. 這種抽樣方法是系統抽樣
C. 這5名男職員的測試成績的方差大于這5名女職員的測試成績的方差
D. 該測試中公司男職員的測試成績的平均數小于女職員的測試成績的平均數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com