
【題目】如圖,四面體ABCD中,△ABC是正三角形,AD=CD.
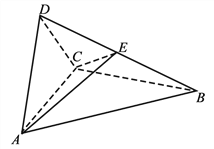
(1)證明:AC⊥BD;
(2)已知△ACD是直角三角形,AB=BD.若E為棱BD上與D不重合的點,且AE⊥EC,求四面體ABCE與四面體ACDE的體積比.
【答案】(1)見解析;(2)1:1.
【解析】試題分析:(1)取![]() 的中點
的中點![]() ,由等腰三角形及等邊三角形的性質得
,由等腰三角形及等邊三角形的性質得![]() ,
, ![]() ,再根據線面垂直的判定定理得
,再根據線面垂直的判定定理得![]() 平面
平面![]() ,即得AC⊥BD;(2)先由AE⊥EC,結合平面幾何知識確定
,即得AC⊥BD;(2)先由AE⊥EC,結合平面幾何知識確定![]() ,再根據錐體的體積公式得所求體積之比為1:1.
,再根據錐體的體積公式得所求體積之比為1:1.
試題解析: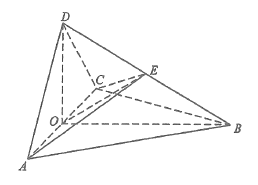
(1)取AC的中點O,連結DO,BO.
因為AD=CD,所以AC⊥DO.
又由于![]() 是正三角形,所以AC⊥BO.
是正三角形,所以AC⊥BO.
從而AC⊥平面DOB,故AC⊥BD.
(2)連結EO.
由(1)及題設知∠ADC=90°,所以DO=AO.
在![]() 中,
中, ![]() .
.
又AB=BD,所以
![]() ,故∠DOB=90°.
,故∠DOB=90°.
由題設知![]() 為直角三角形,所以
為直角三角形,所以![]() .
.
又![]() 是正三角形,且AB=BD,所以
是正三角形,且AB=BD,所以![]() .
.
故E為BD的中點,從而E到平面ABC的距離為D到平面ABC的距離的![]() ,四面體ABCE的體積為四面體ABCD的體積的
,四面體ABCE的體積為四面體ABCD的體積的![]() ,即四面體ABCE與四面體ACDE的體積之比為1:1.
,即四面體ABCE與四面體ACDE的體積之比為1:1.


科目:高中數學 來源: 題型:
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別為240,160,160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動.
(Ⅰ)應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人?
(Ⅱ)設抽出的7名同學分別用A,B,C,D,E,F,G表示,現從中隨機抽取2名同學承擔敬老院的衛生工作.
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設M為事件“抽取的2名同學來自同一年級”,求事件M發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,過點B作⊙O的切線BC,OC交⊙O于點E,AE的延長線交BC于點D. 
(1)求證:CE2=CDCB.
(2)若AB=2,BC= ![]() ,求CE與CD的長.
,求CE與CD的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩運動員進行射擊訓練.已知他們擊中的環數都穩定在![]() ,
,![]() ,
,![]() 環,且每次射擊擊中與否互不影響.甲、乙射擊命中環數的概率如下表:
環,且每次射擊擊中與否互不影響.甲、乙射擊命中環數的概率如下表:

(![]() )若甲、乙兩運動員各射擊
)若甲、乙兩運動員各射擊![]() 次,求甲運動員擊中
次,求甲運動員擊中![]() 環且乙運動員擊中
環且乙運動員擊中![]() 環的概率.
環的概率.
(![]() )若甲射擊
)若甲射擊![]() 次,用
次,用![]() 表示這
表示這![]() 次射擊擊中
次射擊擊中![]() 環以上(含
環以上(含![]() 環)的次數,求隨機變量
環)的次數,求隨機變量![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數f(x)=(|x﹣2|+1)4,給出如下三個命題:①f(x+2)是偶函數;②f(x)在區間(﹣∞,2)上是減函數,在區間(2,+∞)上是增函數;③f(x)沒有最小值.其中正確的個數為( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M、N分別是A1B1、A1C1的中點,BC=AC=CC1 , 則CN與AM所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位安排![]() 位員工在春節期間大年初一到初七值班,每人值班
位員工在春節期間大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位員工中的甲、乙排在相鄰的兩天,丙不排在初一,丁不排在初七,則不同的安排方案共有( )
位員工中的甲、乙排在相鄰的兩天,丙不排在初一,丁不排在初七,則不同的安排方案共有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經市場調查,某種商品在過去50天的銷量和價格均為銷售時間t(天)的函數,且銷售量近似地滿足f(t)=-2t+200(1≤t≤50,t∈N),前30天價格為g(t)=![]() t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天價格為g(t)=45(31≤t≤50,t∈N).
(1)寫出該種商品的日銷售額S與時間t的函數關系式;
(2)求日銷售額S的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com