
【題目】“工資條里顯紅利,個稅新政入民心”.隨著2019年新年鐘聲的敲響,我國自1980年以來,力度最大的一次個人所得稅(簡稱個稅)改革迎來了全面實施的階段.某![]() 從業者為了解自己在個稅新政下能享受多少稅收紅利,繪制了他在26歲-35歲(2009年-2018年)之間各年的月平均收入
從業者為了解自己在個稅新政下能享受多少稅收紅利,繪制了他在26歲-35歲(2009年-2018年)之間各年的月平均收入![]() (單位:千元)的散點圖:(注:年齡代碼1-10分別對應年齡26-35歲)
(單位:千元)的散點圖:(注:年齡代碼1-10分別對應年齡26-35歲)
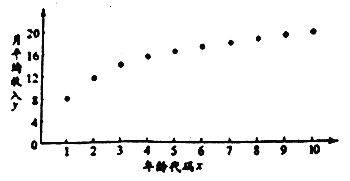
(1)由散點圖知,可用回歸模型![]() 擬合
擬合![]() 與
與![]() 的關系,試根據有關數據建立
的關系,試根據有關數據建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)如果該![]() 從業者在個稅新政下的專項附加扣除為3000元/月,試利用(1)的結果,將月平均收入視為月收入,根據新舊個稅政策,估計他36歲時每個月少繳納的個人所得稅.
從業者在個稅新政下的專項附加扣除為3000元/月,試利用(1)的結果,將月平均收入視為月收入,根據新舊個稅政策,估計他36歲時每個月少繳納的個人所得稅.
附注:①參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②參考公式:回歸方程![]() 中斜率和截距的最小二乘估計分別為
中斜率和截距的最小二乘估計分別為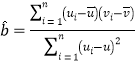 ,
,![]() .
.
③新舊個稅政策下每月應納稅所得額(含稅)計算方法及稅率表如下:
舊個稅稅率表(個稅起征點3500元) | 新個稅稅率表(個稅起征點5000元) | |||
繳稅 級數 | 每月應納稅所得額(含稅) | 稅率 | 每月應納稅所得額(含稅) | 稅率 |
1 | 不超過1500元的都分 | 3 | 不超過3000元的都分 | 3 |
2 | 超過1500元至4500元的部分 | 10 | 超過3000元至12000元的部分 | 10 |
3 | 超過4500元至9000元的部分 | 20 | 超過12000元至25000元的部分 | 20 |
4 | 超過9000元至35000元的部分 | 25 | 超過25000元至35000元的部分 | 25 |
5 | 超過35000元至55000元的部分 | 30 | 超過35000元至55000元的部分 | 30 |
|
|
|
|
|
科目:高中數學 來源: 題型:
【題目】(2017高考新課標Ⅲ,理19)如圖,四面體ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
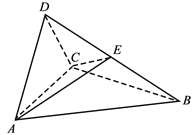
(1)證明:平面ACD⊥平面ABC;
(2)過AC的平面交BD于點E,若平面AEC把四面體ABCD分成體積相等的兩部分,求二面角D–AE–C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解高二學生學習效果,從高二第一學期期中考試成績中隨機抽取了25名學生的數學成績(單位:分),發現這25名學生成績均在90~150分之間,于是按![]() ,
,![]() ,…,
,…,![]() 分成6組,制成頻率分布直方圖,如圖所示:
分成6組,制成頻率分布直方圖,如圖所示:
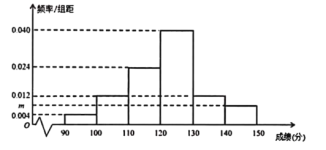
(1)求![]() 的值;
的值;
(2)估計這25名學生數學成績的平均數;
(3)為進一步了解數學優等生的情況,該學校準備從分數在![]() 內的同學中隨機選出2名同學作為代表進行座談,求這兩名同學分數在不同組的概率.
內的同學中隨機選出2名同學作為代表進行座談,求這兩名同學分數在不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有兩個車間生產同一種產品,第一車間有工人200人,第二車間有工人400人,為比較兩個車間工人的生產效率,采用分層抽樣的方法抽取工人,并對他們中每位工人生產完成一件產品的時間(單位:min)分別進行統計,得到下列統計圖表(按照[55,65),[65,75),[75,85),[85,95]分組).
分組 | 頻數 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合計 | 20 |
第一車間樣本頻數分布表
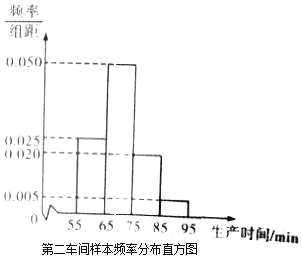
(Ⅰ)分別估計兩個車間工人中,生產一件產品時間小于75min的人數;
(Ⅱ)分別估計兩車間工人生產時間的平均值,并推測哪個車間工人的生產效率更高?(同一組中的數據以這組數據所在區間中點的值作代表)
(Ⅲ)從第一車間被統計的生產時間小于75min的工人中隨機抽取2人,求抽取的2人中,至少1人生產時間小于65min的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,長方體![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 分別在
分別在![]() 上,
上,![]()
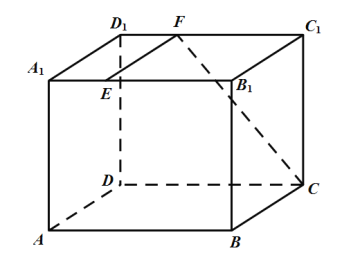
(1)求直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)過點![]() 的平面
的平面![]() 與此長方體的表面相交,交線圍成一個正方形,求平面
與此長方體的表面相交,交線圍成一個正方形,求平面![]() 把該長方體分成的兩部分體積的比值.
把該長方體分成的兩部分體積的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的兩個焦點分別為F1,F2,短軸的一個端點為P,△PF1F2內切圓的半徑為
=1(a>b>0)的兩個焦點分別為F1,F2,短軸的一個端點為P,△PF1F2內切圓的半徑為![]() ,設過點F2的直線l與被橢圓C截得的線段為RS,當l⊥x軸時,|RS|=3.
,設過點F2的直線l與被橢圓C截得的線段為RS,當l⊥x軸時,|RS|=3.
(1) 求橢圓C的標準方程;
(2) 若點M(0,m),(![]() ),過點M的任一直線與橢圓C相交于兩點A.B,y軸上是否存在點N(0,n)使∠ANM=∠BNM恒成立?若存在,判斷m、n應滿足關系;若不存在,說明理由。
),過點M的任一直線與橢圓C相交于兩點A.B,y軸上是否存在點N(0,n)使∠ANM=∠BNM恒成立?若存在,判斷m、n應滿足關系;若不存在,說明理由。
(3) 在(2)條件下m=1時,求△ABN面積的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品公司研發生產一種新的零售食品,從產品中抽取200件作為樣本,測量這些產品的一項質量指標值,由測量結果得到如下的頻率分布直方圖:
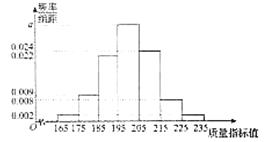
(1)求直方圖中![]() 的值;
的值;
(2)由頻率分布直方圖可認為,這種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,試計算這批產品中質量指標值落在
,試計算這批產品中質量指標值落在![]() 上的件數;
上的件數;
(3)設產品的生產成本為![]() ,質量指標值為
,質量指標值為![]() ,生產成本與質量指標值滿足函數關系式
,生產成本與質量指標值滿足函數關系式![]() ,假設同組中的每個數據用該組數據區間的右端點代替,試計算生產該食品的平均成本.參考數據:若
,假設同組中的每個數據用該組數據區間的右端點代替,試計算生產該食品的平均成本.參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年12月28日,成雅鐵路開通運營,使川西多個市縣進入動車時代,融入全國高鐵網,這對推動沿線經濟社會協調健康發展具有重要意義.在試運行期間,鐵道部門計劃在成都和雅安兩城之間開通高速列車,假設每天7:00-8:00,8:00-9:00兩個時間段內各發一趟列車由雅安到成都(兩車發車情況互不影響),雅安發車時間及其概率如下表所示:
第一趟列車 | 第二趟列車 | |||||
發車時間 | 7:10 | 7:30 | 7:50 | 8:10 | 8:30 | 8:50 |
概率 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
若小王、小李二人打算乘動車從雅安到成都游玩,假設他們到達雅安火車站候車的時間分別是周六7:00和7:20(只考慮候車時間,不考慮其它因素).
(1)求小王候車10分鐘且小李候車30分鐘的概率;
(2)設小李候車所需時間為隨機變量![]() ,求
,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com