
已知函數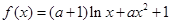 .
.
(Ⅰ)討論函數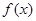 的單調性;
的單調性;
(Ⅱ)設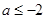 ,證明:對任意
,證明:對任意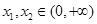 ,
,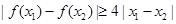 .
.
(Ⅰ)分類討論得到單調性 (Ⅱ)構造函數用導數的方法證明.
【解析】
試題分析:(Ⅰ) f(x)的定義域為(0,+ ),
),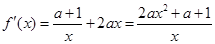
當a≥0時,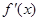 >0,故f(x)在(0,+
>0,故f(x)在(0,+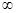 )單調增加;
)單調增加;
當a≤-1時,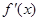 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+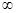 )單調減少;
)單調減少;
當-1<a<0時,令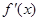 =0,解得x=
=0,解得x=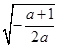 .當x∈(0,
.當x∈(0, 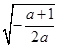 )時,
)時, 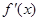 >0;
>0;
x∈(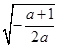 ,+
,+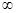 )時,
)時,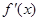 <0, 故f(x)在(0,
<0, 故f(x)在(0, 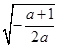 )單調增加,在(
)單調增加,在(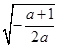 ,+
,+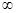 )單調減少
)單調減少
(Ⅱ)不妨設x1≥x2.由于a≤-2,故f(x)在(0,+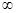 )單調減少.
)單調減少.
所以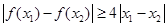 等價于
等價于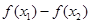 ≥4x1-4x2,
≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,則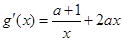 +4=
+4=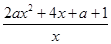 .
.
于是 ≤
≤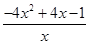 =
=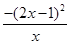 ≤0.
≤0.
從而g(x)在(0,+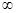 )單調減少,故g(x1)
≤g(x2),即 f(x1)+ 4x1≤f(x2)+
4x2,
)單調減少,故g(x1)
≤g(x2),即 f(x1)+ 4x1≤f(x2)+
4x2,
故對任意x1,x2∈(0,+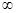 ) ,
) ,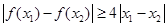 .
.
考點:利用導數求閉區間上函數的最值;利用導數研究函數的單調性.
點評:本題考查利用導數研究函數的單調性及函數的最值問題,考查分類討論思想,考查學生綜合運用知識分析問題解決問題的能力,屬難題.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com